Top Addition Strategies: The Place Value Strategy

Today, we’re digging into our fourth addition strategy. We are examining Place Value. *Record Scratch* Place Value as an addition strategy? Yes! The Place Value Strategy.

Before I continue, let me fill you in. So far, we’ve covered three addition strategies. Those include:

• The Compensation Strategy
• The Transformation Strategy
• The Decomposition Strategy

In the previous posts, I emphasized the importance of students learning these strategies naturally. There are other ways to support our students without explicit instruction. And the Place Value Strategy is no exception.

You might be wondering at this point: Isn’t explicit instruction our job as a teacher? Our job is to support student learning. And, over the years, I’ve learned that doesn’t always mean explicit teaching. Instead, it means providing students with able resources to support them, lead them, and challenge them. When you see a student ready to use the place value strategy, point it out!

But, before you do that, it is important to know what the place value strategy looks like in each grade and become deeply familiar with it yourself.

Let’s take a look at the Place Value Strategy so we can better identify it when we see it with our students. Are you ready?

What is the Place Value Strategy for Addition?

You’re probably familiar with Place Value. Teaching place value begins early in our math learning journeys, as we build an understanding of how the position of a digit within a number changes its value.

Students who have a solid grasp of place value may start to apply that understanding to addition problems, evolving into the place value strategy.

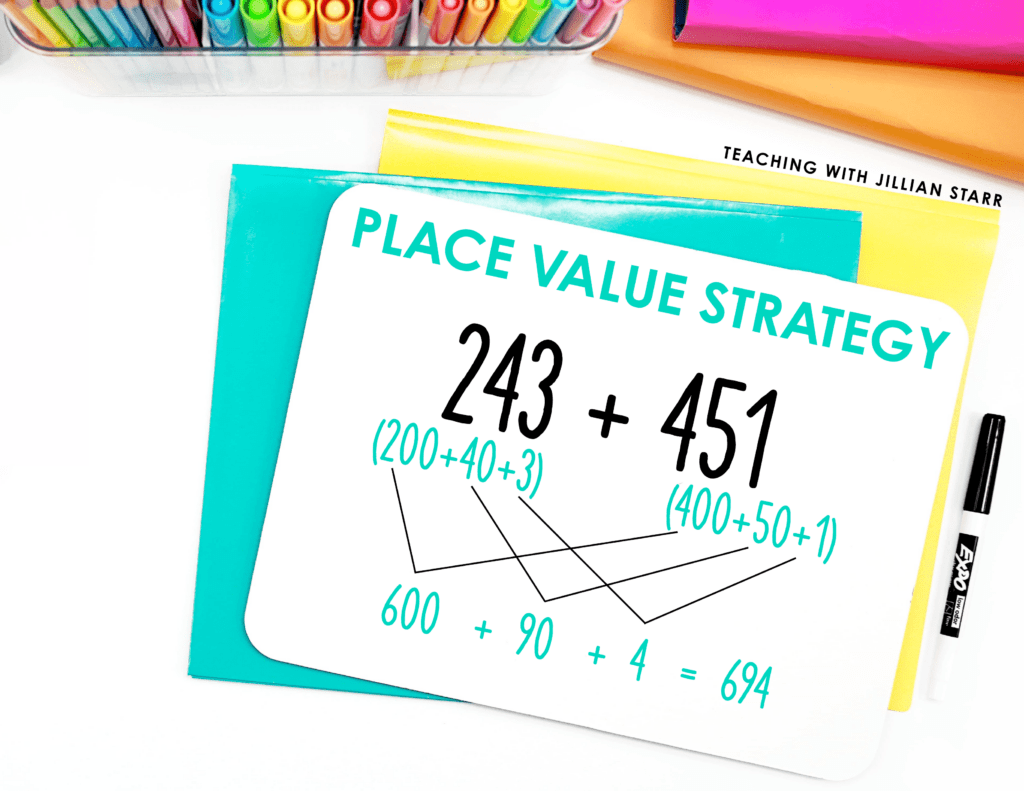
The place value strategy involves breaking apart numbers by place value, also known as expanded form. For example, the number 243 can be broken down into 200+40+3.

Then, students systematically add by place value. Let’s use 243+451 as an example.

First, students will add the hundreds: 200+400=600. Next, they will add the tens: 40+50=90. Then, they will add the ones 3+1=4. Finally, students will add these numbers together: 600+90+4=694.

What Does the Place Value Strategy Look Like in First Grade?

You might be thinking: How does this apply to first grade? After all, students are still building number sense and growing their understanding of place value.

True. In first grade, students discover how place value works. And when it comes to addition, they are typically working with adding and subtracting through twenty. Not many digits to work with. Often, they are still using tens frames and a lot of manipulatives.

Bingo! That’s where you begin! Our job in first grade is to build number sense by helping them see relationships between numbers, and develop a strong understanding of place value.

Many math manipulatives for first grade are designed to help students understand addition through place value. In first grade, the place value strategy looks like:

• Breaking down two-digit numbers into tens and ones with Unifix cubes or base ten blocks
• Adding numbers with tens frames.
• Begin noticing patterns related to place value on a hundred chart

What Does the Place Value Strategy Look Like in Second Grade?

Students in second grade build on their work with two-digit numbers. This can look like 42+7 (a double-digit plus a single-digit) or 42+37 (two double-digit numbers).

With 42+7 the numbers are first broken down into expanded form: (40+2)+7. Students can add the ones, 2+7=9, and then add those back onto 40. 40+9=49.

When we look at 42+37, its expanded version becomes (40+2)+(30+7). Students will add their tens together, 40+30=70. Then add their ones 2+7=9. Finally, they can combine their expanded parts 70+9=79.

What Does the Place Value Strategy Look Like in Third Grade?

In third grade, most students have a pretty strong understanding of place value though the hundreds place. They may be inclined to start using this understanding to support them with larger numbers in addition.

Let’s say the problem is 254+533. In order to make the problem friendly, a student might start naturally breaking them apart and adding like numbers together: “I know that 200+500=700, 50+30=80, and 4+3=7.” Then, they might add those numbers together.

However, on paper, this can start to get messy. During a Number Talk, if a child demonstrates the use of the place value strategy, you can model how to organize this way of thinking: Stacking one on top of the other, making sure to align the place values. Then, you can show them what it looks like to add numbers vertically.

Note: This is not a lead into the traditional algorithm, nor are we looking to push or connect this to what some students may already know about the traditional algorithm. We’ll talk more about this next time!

However, I’ve seen this happen time and time again. Students start stacking their numbers, but they are misaligned. The ones of a number align with the tens of another. They are writing the numbers in different sizes. Make sure to emphasize the importance of stacking place values. Ones on top of ones. Tens on top of tens. And ensure that when writing, their numbers are about the same size

Closing Thoughts on Place Value as an Addition Strategy

You might be wondering: How will students learn how to fully use the Place Value Strategy without explicitly teaching it to students?

The place value strategy looks very different depending on the grade level. But, at each stage, students build a better understanding of place value and its role in the addition process.

There are many ways in which we can support and guide students without explicit instruction.

• Encourage students to recognize their own strategies
• Reflect on their own math process
• Work to articulate that process to their peers
• Allow other students to be inspired to try a new strategy that may be more efficient than their own

Our role is to build students number sense, place value, and help them begin to understand the strategies they are using. As we see these strategies being used in our classrooms, we can most certainly call attention to them and highlight them in front of other students.

As students are ready they will begin to understand and try on more and more efficient strategies. It’s a process that we don’t want to rush or force.

EXCITING NEWS!

First Grade Teachers, something big is coming! If you’re someone who loves digging into math concepts, or wants to become a better math teacher for your students, I’d love for you to join me. If you’d like to be the first to find out more, enter your info below!