

When it comes to teaching fractions, we often visualize them using a circle divided into equal-sized pieces like a pizza – a relatable image for most students! However, it’s equally important to help students understand fractions of a set, rather than just parts of a whole, especially as they move into the upper elementary grades.
Getting Started: What are fractions of a set?
Fractions of a set involve a group of objects that can be divided into equal parts, and we can name the value of one or more of the groups using a fraction. For instance, in this image of connecting cubes, ⅓ of the cubes are pink, which means that ⅓ of 12 cubes is 4. The 12 represents the total number of cubes, the 4 represents the pink cubes, and the ⅓ represents one of the 3 equal groups we get from dividing the 12 cubes with each group containing 4 cubes.
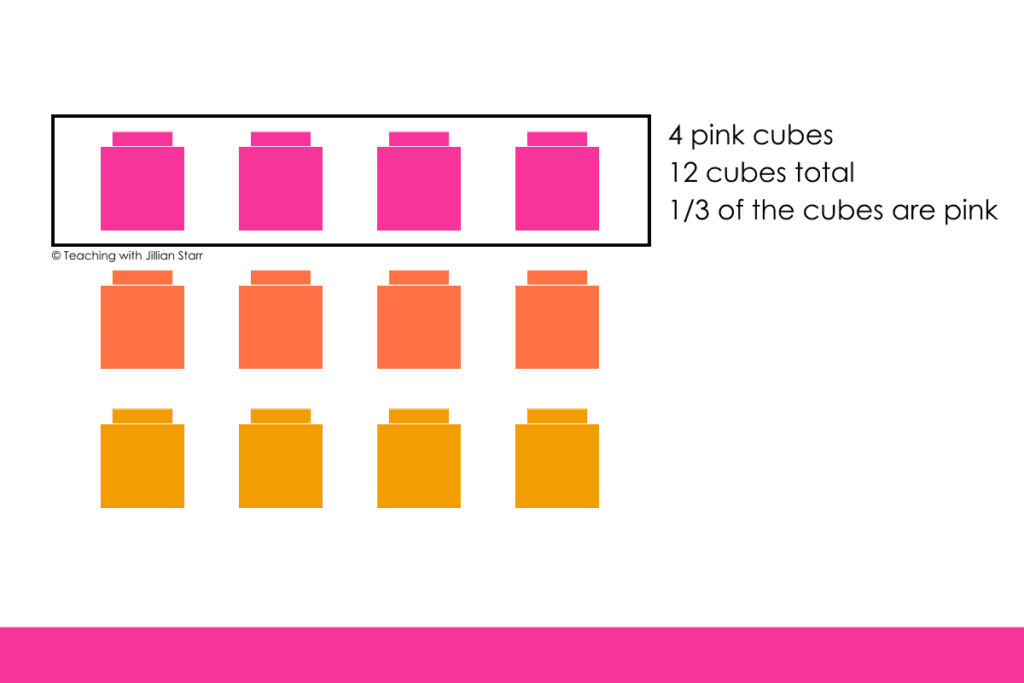
Today I’m going to share my top 4 tips for teaching fractions of a set to help students master this concept. Let’s get to it!
1. Build Conceptual Understanding of Fractions of a Set
My first tip is to emphasize conceptual understanding over procedures. As with all math topics, when students grasp what is really happening, the procedures they learn later make much more sense and they will not have to rely on memorization.
Students officially begin to interact with fractions of a set beginning in third grade, but really, kids have been encountering these kinds of problems since they started sharing toys as young kids.
Imagine this scenario: Three kids are playing with 12 toy cars and decide that they should share them. They take the 12 toy cars and divide them equally between the three friends (let’s just assume everyone is in the mood to share!). Little do they know that they just solved the problem ⅓ of 12!


Emphasizing conceptual understanding not only supports later work with procedures but also makes the concepts meaningful for students.
2. Provide Relatable Contexts for Fractions of a Set
Speaking of making concepts meaningful…Tip number two is to use relatable contexts that mirror real-life situations. Without context, fractions of a set can seem disconnected from real life and like an impractical math skill. But in real life? Fractions of a set are everywhere!
Let’s take a look. There is a certain time when kids are always encountering fractions of a set: when they are sharing! At first glance, it may seem that these contexts are introducing division and, well, you’re right! Fractions and division are intertwined but students do not need to truly understand fractions as division until fifth grade.
What if rather than providing students with an image on a worksheet and asking students to find ⅓ of the picture, we gave students word problems and asked students to draw the model (we’ll talk about models shortly)? After trying this in my own classroom, I was AMAZED at the difference I saw in student understanding.
Don’t worry, I’ve got you covered! Here are a few examples of word problems you can use right away:
- My family was sharing French fries for dinner. We had a bag of 40 French fries and each person got ¼ of the fries. How many fries did each person get?
- I have 10 pairs of pants in my dresser. ⅕ of them are leggings. How many leggings are in the drawer?
- ½ of the books I read last year were realistic fiction books. I read 36 books. How many of the books I read were realistic fiction?
- The deck of cards has 33 cards. If each player gets ⅓ of the cards, how many cards does each player get?
- My brother was sharing his toy cars with his cousins. There were 12 toy cars and each boy got 4 cars. What fraction of the cars did each boy get?
You know that old saying “A picture is worth a thousand words?”. Let me tell you, this is SO true when it comes to teaching fractions of a set. Grab an image of a set of objects (any image will do!). You could easily wander around your home or classroom and take photos of groups of objects. Below is an image of some counters.


I can use this image as a warm-up to the day’s math lesson asking students, “How many do you see?” Some students will immediately count the entire set. Others might count how many of each color there are. Still, others might make a connection to fractions and name a fraction to describe how many. Even if students do not make the connection to fractions themselves, we can simply ask them to name the fraction of blue counters, for example. One simple image can lead to a very rich discussion!
3. Utilize Models of Fractions of a Set
Models – manipulatives, pictures, and drawings – are some of your best tools to represent what is happening when we determine the fraction of a set.
Provide manipulatives – or any objects really! – to model problems. Why? Physical objects are easy to move and rearrange. This tactile component provides the opportunity for increased student engagement. On the other hand, when students use a picture of objects or even their own drawing, it can lead to lots of erasing and restarting, which can frustrate our learners.
So what might using models look like? Let’s say we’ve asked students to solve ⅓ of 12. First, students would take out 12 objects such as counters. Then, they would have to separate the 12 counters so that they have 3 equal groups. Using the counters allows students to attempt equal groups by easily moving them around and checking to see if their attempt was correct.
If this was a paper-based task, a student might draw 12 stars, and then circle a set of stars to try to make three equal groups. However, if their first attempt doesn’t work, they’ll have to erase and start over – ugh!
Once students have solved a problem using manipulatives, they can then show their thinking on paper by drawing what they did with the counters. Making the connection between manipulatives and drawings will support their ability to flexibly move back and forth between them.
Eventually, students will be able to use just pictures to solve some problems. That doesn’t mean they should never use manipulatives again though! Students should be allowed to move between the two depending on the problem, putting the ownership onto the student to decide when a particular approach makes the most sense.
4. Investigate Patterns within Fractions of a Set
Fractions of a set are related to fraction multiplication but students don’t need to multiply fractions by whole numbers until 4th and 5th grade. So where does this leave us? Instead of teaching students those procedures early, we can continue to strengthen conceptual understanding by investigating patterns.
Take a look at these problems:
½ of 16 is 8
⅓ of 12 is 4
¼ of 20 is 5
⅕ of 10 is 2
I love this investigation as a warm-up activity. Begin by asking students to share what they notice and what they wonder to get them thinking about the patterns in these problems. They may notice that each fraction is a unit fraction or that the answers are all smaller than the other whole numbers in the problem.
To deepen the discussion, I might ask students how the digits in the fraction and the whole number relate to the answer. Even third graders can recognize that 16 divided by 2 is 8 and 12 divided by 3 is 4. Noticing these patterns can help lay a foundation for the more complex work in 5th grade.
Teaching fractions of a set doesn’t have to be a worksheet overload and, truthfully, it’s so much better when it’s not! These four tips have helped my own students to master fractions of a set and I hope you find success with them too. Do you have a favorite tip for teaching this concept? Let us know!
Looking for even more ideas about fractions? Check out all of our fraction articles here!











Leave a Comment