
I’ve been spending a lot of time thinking about multiplication and how to build students’ fluency with math facts (clearly!). By now, you know that I strongly believe that we need to build students’ conceptual understanding of multiplication, including building arrays, “groups of” representations, and area models. Only after they have a strong grasp of these concepts can we expect students to progress toward becoming more fluent with math facts.
If you missed my last two blog posts about when to use a multiplication chart and starting with a blank multiplication table, I highly recommend you check those out because today’s topic of math facts builds on those posts.
What Does it Mean to be Fluent with Math Facts?
The Common Core State Standards talk about fluency across grade levels, but its meaning can be perplexing for teachers. Unfortunately, people often equate fluency of math facts with students correctly answering them quickly, which has led to the infamous “mad minute” type worksheets. However, fluency is much more than that. It actually builds on students’ conceptual understanding of the operation and encompasses efficiency, accuracy, and flexibility.
Once students can accurately and efficiently solve math fact problems and explain how others might solve them to demonstrate their flexibility, they can be considered fluent. Yet, it’s essential to clarify that fluency is not the same as automaticity, which comes after all of this work. Don’t worry – I’ll touch on automaticity later.
Progressing Toward Fluency with Math Facts
We can build students’ multiplication fluency by explicitly teaching them strategies for solving math facts, highlighting the relationships between different facts and strategies, and repeatedly modeling these strategies using manipulatives. Afterward, students should be given ample time to practice using these strategies and explain their reasoning for selecting one strategy over another. This approach builds upon students’ conceptual understanding to accurately solve problems while being flexible in their thinking.
To demonstrate efficiency, students need to be thoughtful about the strategies they select when solving problems. Selecting a strategy is also an opportunity for students to demonstrate their understanding of the commutative property. When selecting a strategy, students may decide to solve the related multiplication fact in order to select a strategy that helps them find the product more efficiently.
For example, when solving 5 x 7, students might think of this as 5 groups of 7 and then add 7 + 7 + 7 + 7 + 7. While repeated addition can result in an accurate answer, using the commutative property to solve 7 x 5 or 7 groups of 5 would be more efficient for most students because of their ability to easily count by 5s. It’s crucial to emphasize that different strategies may be more efficient in specific scenarios.

Multiplication Mega Pack
Explicitly Teaching Strategies for Math Facts
Students who rely solely on skip counting as a strategy for solving multiplication math facts aren’t yet fluent even if they can find the correct answer quickly. If skip counting or repeated addition are their only strategies for solving math facts, they are not meeting the flexibility criteria for fluency. These two strategies are not particularly efficient and do not lend themselves to being flexible. Skip counting might be an efficient strategy for some facts, such as x5 and x10, but less so for x7 and x8, leading to reduced accuracy.
So, let’s dig into other strategies students can use to work towards multiplication fluency! Keep in mind that students should already have a solid foundation of conceptual understanding of multiplication. Because these strategies are more abstract, that solid foundation allows them to connect to the strategies to their conceptual understanding.
It’s also important to note that students internalize strategies far greater when they discover them independently. A great way to guide these discoveries is through Number Talks! By choosing a strategic multiplication expression on the board and opening it up to discussion, students will naturally share how they solved the problem. After hearing a variety of responses, you can highlight a strategy that you want to reinforce more explicitly.
Let’s take a look at what some of those explicit highlights can look like.
Multiplying by 1, 10, and 5
I don’t think anyone will argue with 1s, 10s, and 5s math facts being easiest for students. Students often recognize the patterns in the 1 and 10 times tables quickly, especially when exposed to activities like choral counting by 1s and 10s in the lower grades. The key is to record the count and ask students to discuss the patterns they observe. Similarly, by the time students are learning the 5 multiplication math facts, they’ve likely been skip counting by 5s for a while, which supports fluency with 5 facts.
One word of caution when teaching students to multiply by 10 is the phrase “add a 0.” I have learned to avoid this phrase because it can hinder students’ number sense and place value understanding. Consider what adding a 0 really means. If you add a 0 to 2, do you get 20? Of course not! Students have known that adding a 0 to a number does not change the value of that number for many years at this point and it can muddy their understanding to now suggest that when solving 2 x 10, students can add a 0 to 2 to get 20.
Additionally, when students are multiplying by 10, saying that they are adding a 0 isn’t accurately reflecting what is happening. I won’t get on my soapbox today… I’ll just say that there are some complex place value concepts at play and “add a 0” is one of those pesky things we teach kids that we have to undo later in their math learning. Better to avoid it altogether!
I have updated our FREE Multiplication Math Facts Strategy Poster to reflect this important note. You can get it by clicking the button below!





Multiplication Strategy Chart
Help your students master those tricky multiplication facts with these strategies!
Multiplying by 2, 4, and 8
When teaching students to multiply by 2, provide opportunities for them to see that it is the same as a doubles addition fact. Have students represent facts like 8 x 2 (or 2 x 8, commutative property!) as two equal groups of 8, which can be written as the addition expression 8+8. Provide students with opportunities to repeat these activities with many multiplication math facts to reinforce the connection to doubles addition facts.
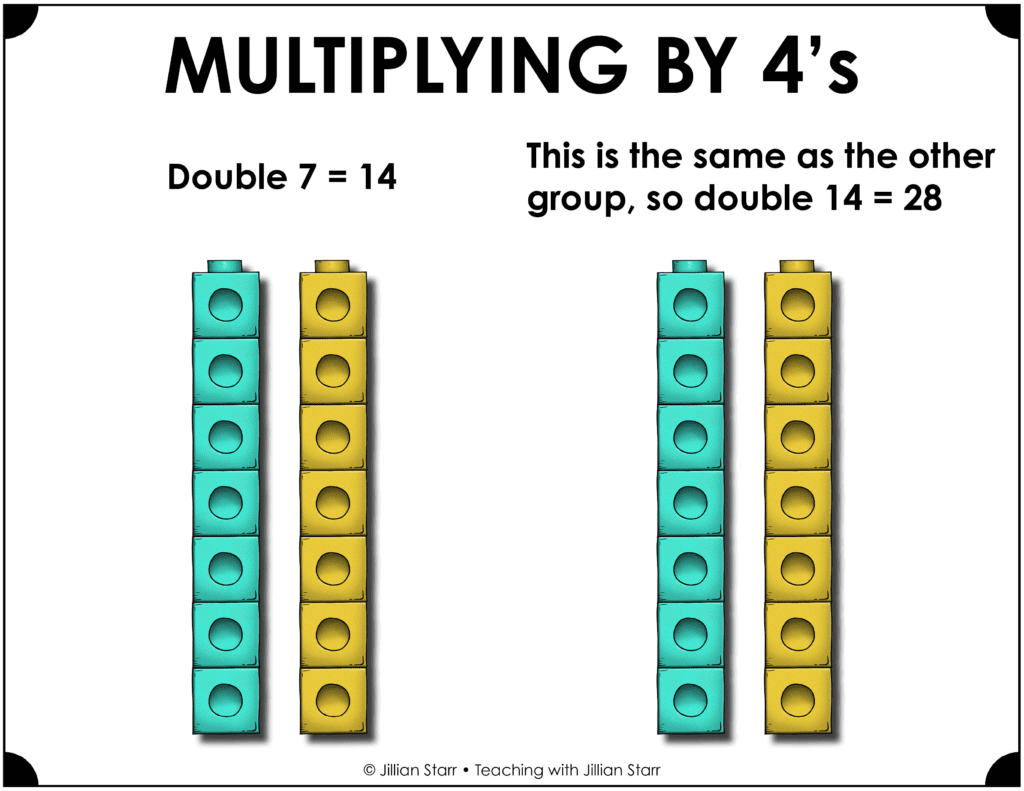

Multiplying by 4 and 8 connects directly to doubling or multiplying by 2. To solve x4 facts, students can double the other factor and then double again. For example, when solving 7 x 4, double 7 to get 14 and then double 14 to get 28 so 7 x 4 = 28. Again, it’s important to allow students to see this strategy visually. Have students represent 7 x 4 using 4 groups of 7 connecting cubes. Separate that group into two sets: 2 groups of 7 and 2 groups of 7. Now students can see that the 7 is doubled twice resulting in two 14s or 14 doubled.
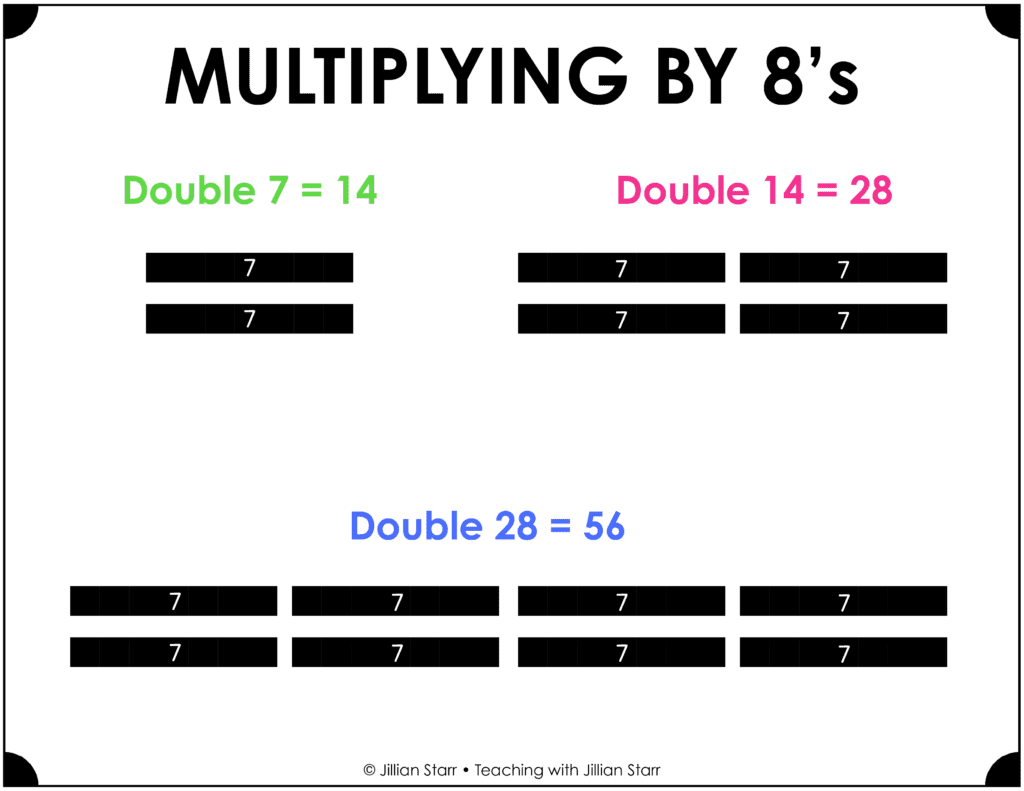
To multiply by 8, the strategy of double, double, double can be very efficient. It’s more manageable than it sounds! Let’s take 7 x 8 or 8 x 7. Using this strategy for multiplying by 8, first, we double 7 to get 14 (i.e. 2 x 7). Then double that again to get 28 (i.e. 4 x 7). Finally, we double one more time: 28 + 28 is 56 to determine 7 x 8 = 56. Again, it’s important to provide students the opportunity to visualize this strategy. Another manipulative that can be helpful in modeling multiplication strategies is Cuisenaire rods. Below you’ll see the black 7 rod modeling 8 x 7.

Multiplying by 3 and 6
When multiplying by 3 and 6, students leverage the relationships with other math facts. When multiplying by 3, students can see it as two times or doubling the other factor and then adding one group of that factor. For example, 3 x 7 is the same as 2 x 7 (or 7 doubled) and then another group of 7.
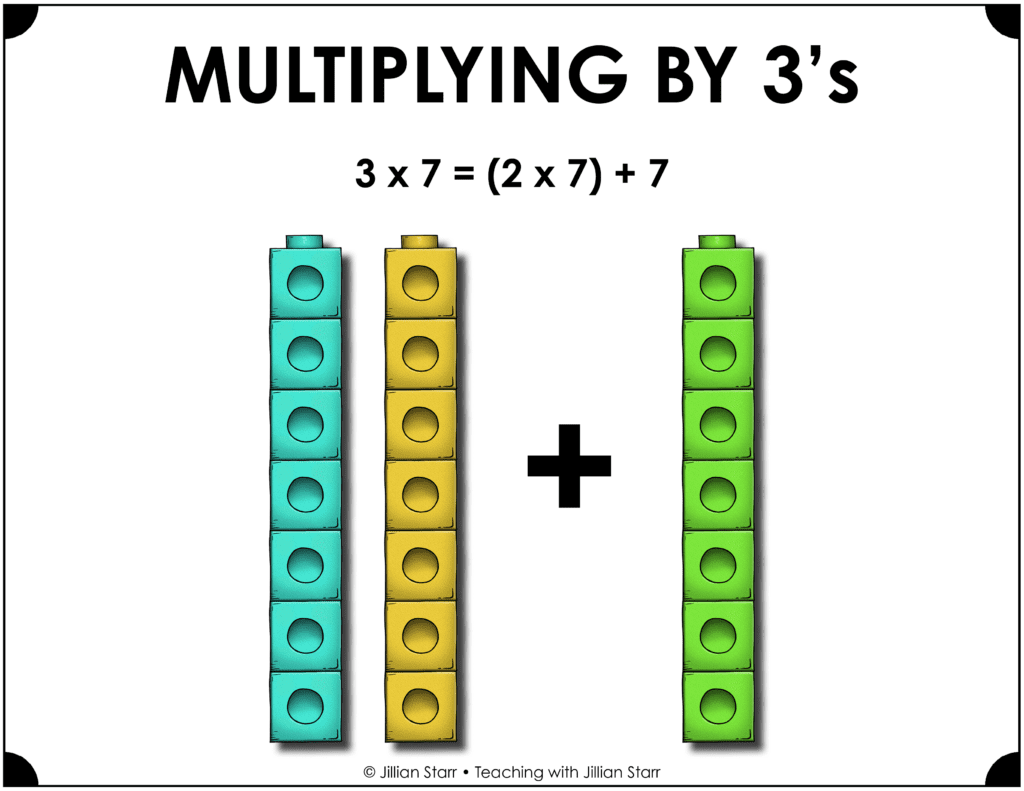
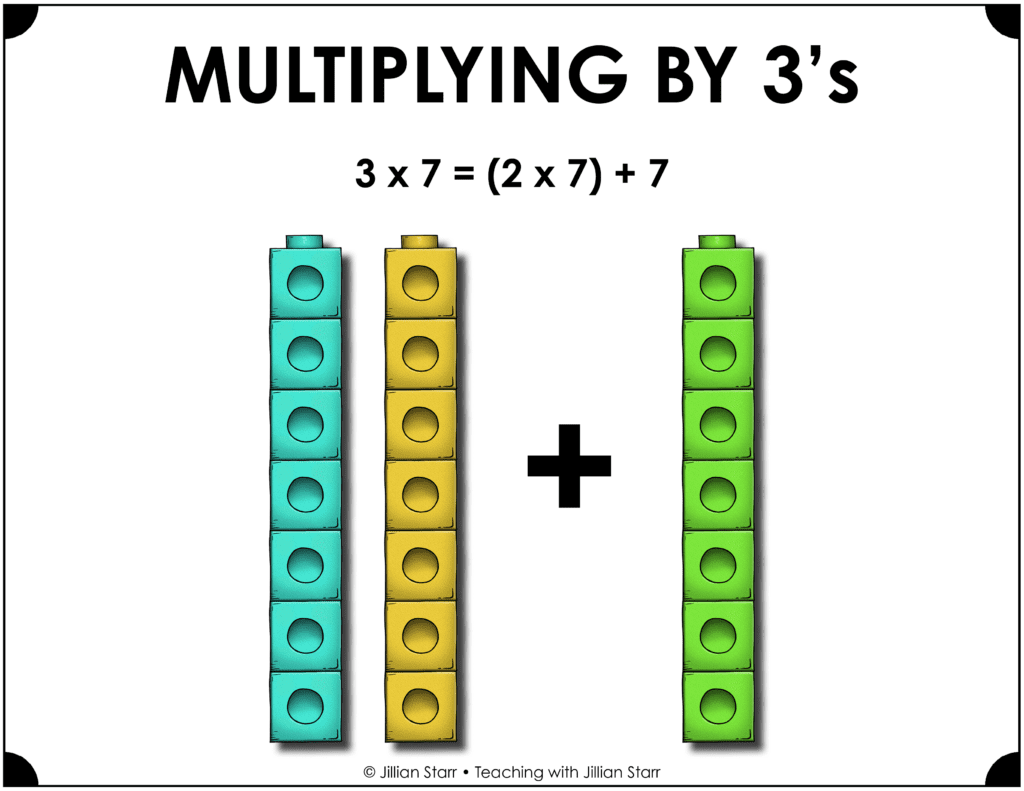
Similarly, when multiplying by 6, students can multiply the other factor by 5 and then add another group of that factor. For instance, when solving 6 x 7, students can solve 5 x 7 to get 35 and then add another 7 to get 42.
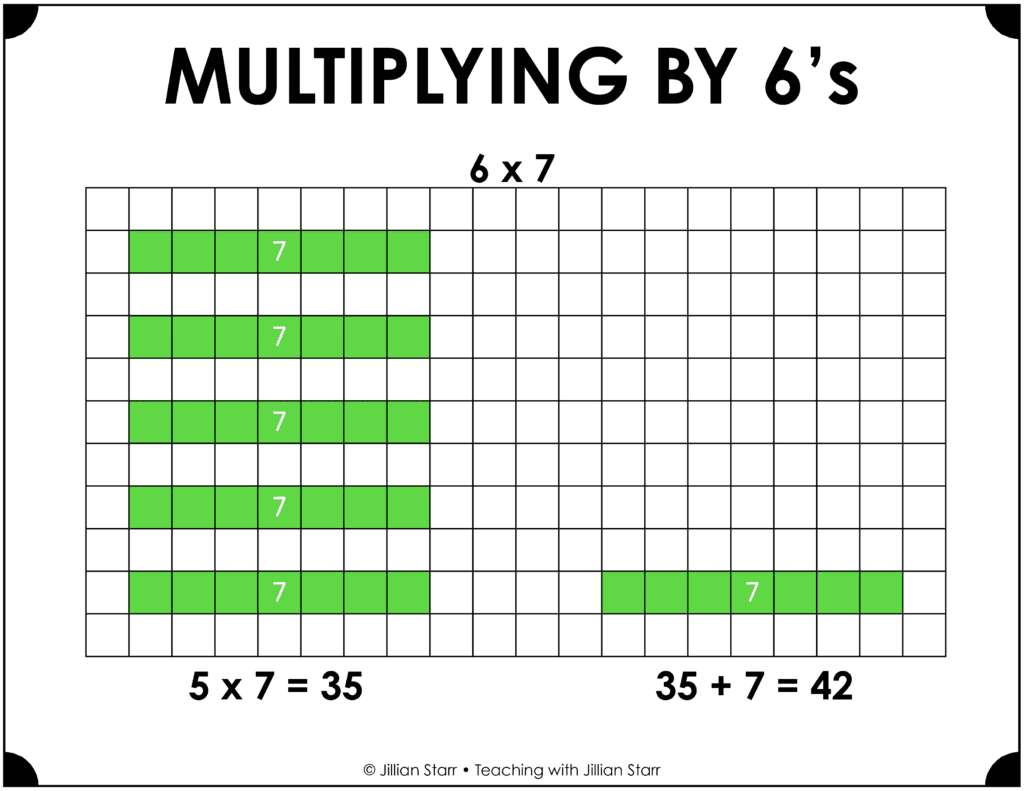

This relationship is not the only one for multiplying by 6 however. Students could also multiply the other factor by 3 and then double it. Let’s look at 6 x 7 again. Using this strategy, students solve 3 x 7 to get 21 and then double it to get 42. It’s all about connecting problems to more familiar problems and finding the most efficient path!
By now you know what I’m going to say: model it! Ask students to model these math facts and strategies to support internalizing these strategies. Below are some example images of models for multiplying by 3 and 6.
Multiplying by 9 and 7
Related math facts are also helpful when multiplying by 9 and 7. To multiply by 9, multiply the other factor by 10 and then subtract one group of that factor. So if solving 7 x 9, multiply 7 by 10 to get 70 and then subtract 7 to get 63.
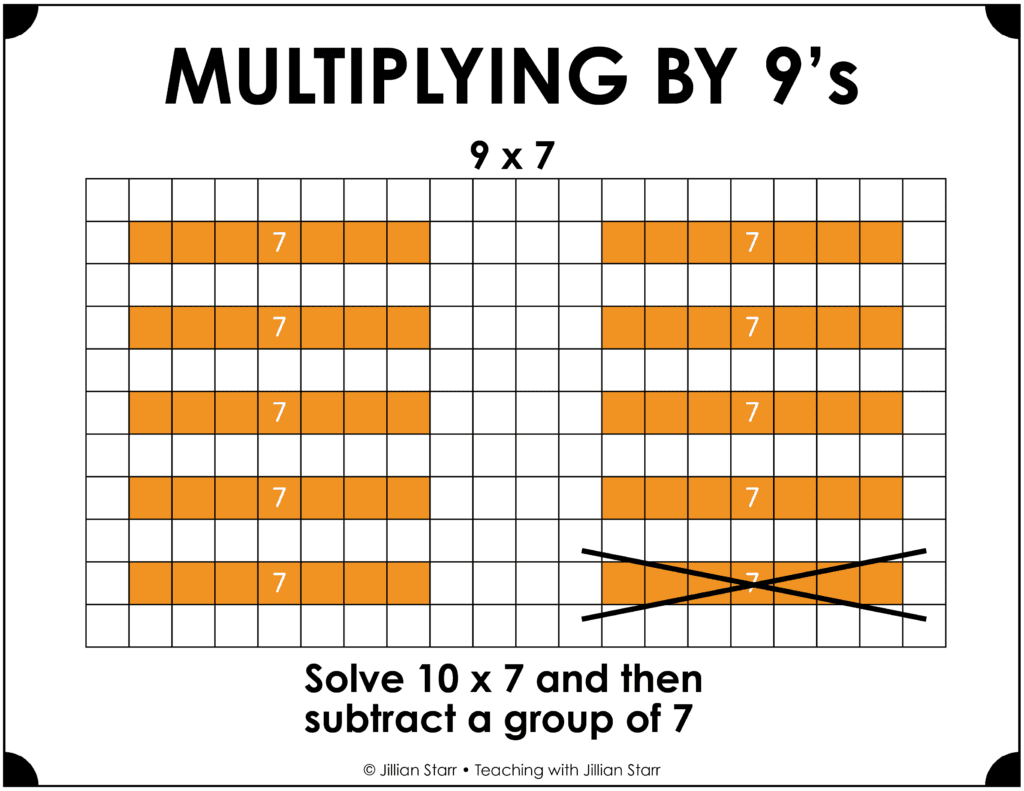

You may also be familiar with the 9’s hand trick. While the trick can be helpful in getting a product very quickly and accurately, it does not support students’ number sense so we want to make sure to also teach other strategies.
Multiplying by 7 is often the hardest for students! However, we can decompose the 7 into 5 and 2, two factors that tend to be significantly easier for students. If a student is solving 7 x 7, they can decompose one 7 into 5 and 2 to multiply, 5 x 7 and 2 x 7, much easier problems. Then they add the products, 35 and 14, to get 49.
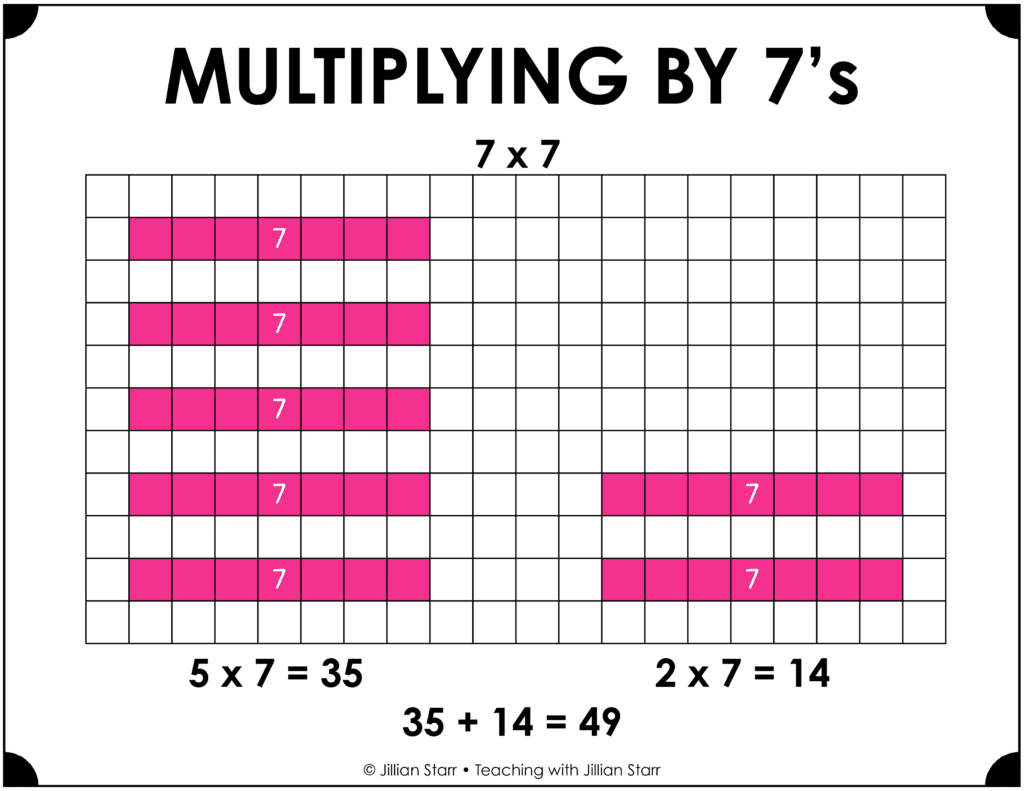

Multiplying by 11 and 12
Finally, we have the 11 and 12 times tables. Again, decomposing comes in very handy here. Students can decompose these numbers into 10 and 1 or 10 and 2, factors that are more manageable for students. For example, 7 x 12 can be solved by solving 7 x 10 and 7 x 2 and then adding those products to get 70 + 14 or 84.
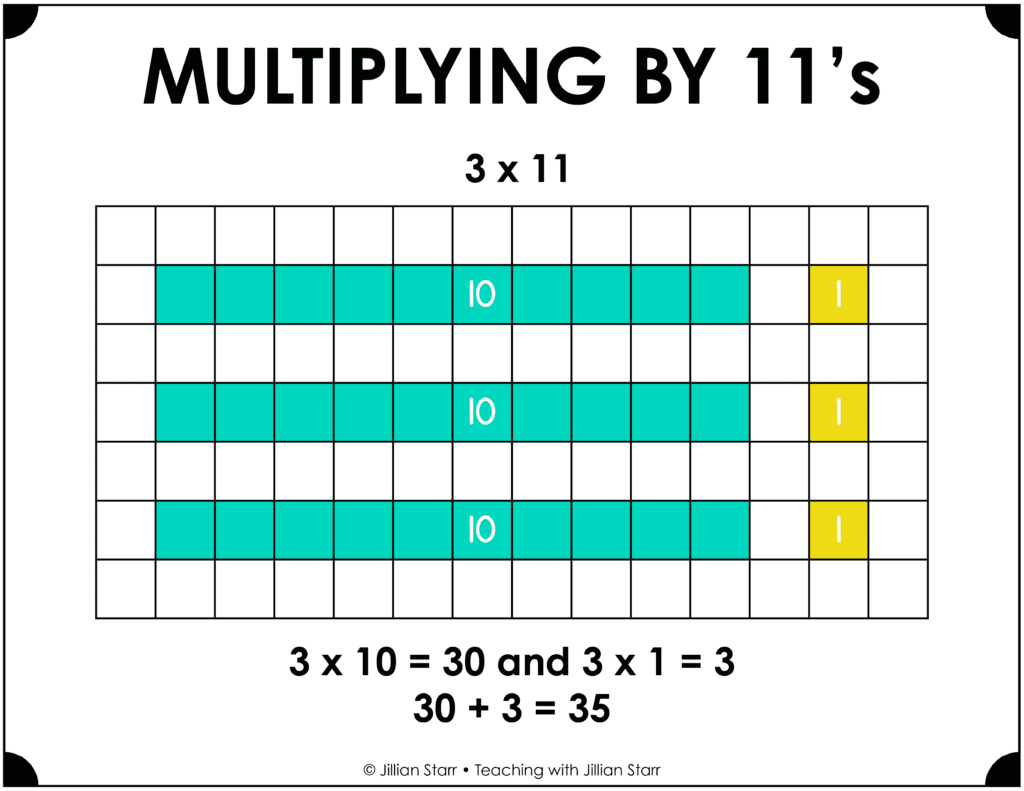

Similar to learning the 1 and 10 times tables, students can also become familiar with the pattern in the 11 times table. Again, to support this pattern recognition, we need to provide students with opportunities to see the patterns during choral counting and by studying the multiplication table.
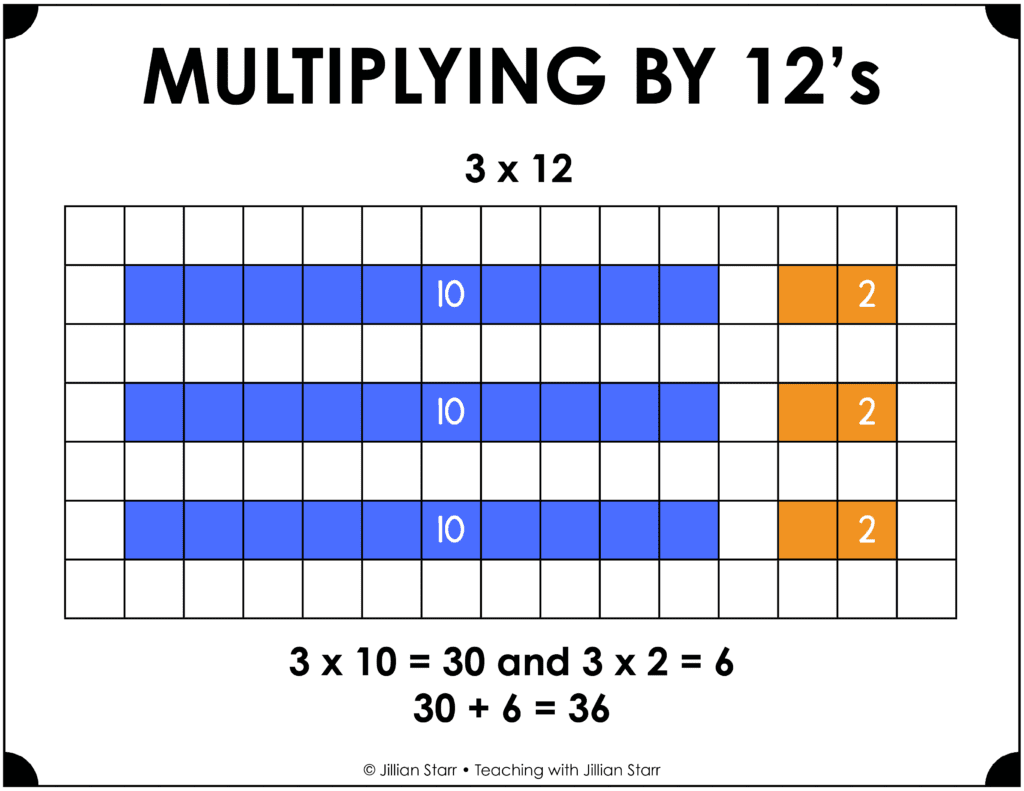

As I mentioned earlier, none of these strategies are the strategy to use. Instead, students must consider the problem they are solving to select a strategy that will not only accurately yield a product, but also be efficient. Emphasize the importance of being thoughtful when selecting a strategy by continually asking students to explain why they selected specific strategies rather than focusing on whether the product is correct or incorrect.
Automaticity with Math Facts
Okay, so what about automaticity?! Automaticity will come. I know, not the answer you might want to hear but as students practice using these strategies and solving a variety of problems in context, students will begin to “just know” math facts. Once students are truly fluent in the true definition rather than just automatic, then we can begin to practice math facts more in isolation using things like games rather than connected to conceptual understanding.



Multiplication Mega Pack
Knowing multiplication math facts automatically certainly has its place. It can reduce the cognitive load for students when solving more complex problems. If a student is solving a multi-step word problem, they need to read the problem, understand the situation, determine what the problem is asking, determine how they might approach the problem, and finally, solve it.
There are so many steps for students to complete before even getting to any calculations. If students then need to use multiple strategies to solve math facts, that problem becomes very mentally taxing and could lead to errors. If students know their math facts automatically, solving that problem becomes just a bit easier for them.
And there we go – moving beyond skip counting to become fluent, no timed tests needed! If you’d like a free multiplication fact strategy poster, scroll to the bottom of the page linked above to get it. Do you have any other helpful strategies for solving multiplication facts? Share below so I can learn from you!





Multiplication Strategy Chart
Help your students master those tricky multiplication facts with these strategies!










Leave a Comment