
Those who have followed me for a while know that I’m on a mission to teach students that math can be found everywhere. Math is not just limited to a daily academic block and repetitive facts learned at home. Math describes the world around us. One of the most convincing pieces of evidence is multiplication arrays.
How to introduce these in a real-life context? Enter: math scavenger hunts.
Math scavenger hunts are a simple way to lead students to discover math patterns in the “real world.” They are exciting and tangible, requiring students to look closely and explore. Today, I will guide you through this three-step series of lessons. It is one of my favorite hands-on multiplication activities.
Even more important: it results in a classroom of students who really know the concept of a multiplication array.
The WHY: Multiplication Arrays and Their Power
Let’s start with the basics. I’ve heard questions from teachers about why we should spend a significant amount of time on multiplication arrays. Here’s the not-so-short answer.
It Starts with Mathematical Representation
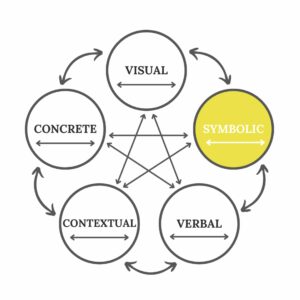
I’ve identified some of the problems of a simplistic three-representation model of mathematical thinking and development in my mathematical representation series. One thing is clear: Students who notice “real world” math patterns are often the same students who more quickly see and develop abstract (symbolic) understandings of mathematical concepts. Multiplication, and the underlying multiplication processes, are no exception.
Students build mathematical understanding through multiple stages of representation: Concrete Representation→ Visual Representation → Symbolic Representation → Verbal Representation → Contextual Representation
If a student does not have a solid grasp of one representation, it can impact their entire understanding of a core mathematical concept.
Multiplication Arrays Bridge the Representations
Multiplication arrays are arrangements of equal rows or columns representing or matching the numbers in a multiplication equation. For example, in equation 3 x 5, there are 3 rows of 5. They can be found literally everywhere. And they can be replicated through multiplication activities that involve manipulatives and visuals.
Multiplication arrays are not just pictorial, visual representations of multiplication. They are physical (concrete) manifestations of math in our daily lives (contextual).
What does that mean? They exemplify and carry students through multiple stages of math through one experience.
Hear me out.
- A concrete representation of math is something physical that can be touched and manipulated.
- A pictorial representation of math translates the concrete example into a two-dimensional visual.
- A contextual representation of math is a real-world example in the 3D plane.
Multiplication arrays are all of those.
There are multiple ways in which concrete versions of multiplication arrays enter the everyday lives of our students.
- Rows of windows on a skyscraper
- Tiles on the floor
- Checkerboards
- A set of Unifix cube sticks
All of these are physical, concrete examples of math.
Multiplication arrays can also be shown as a visual, pictorial representation. Students see pictorial depictions of multiplication arrays regularly:
- Grids
- Equal rows of a symbol or image
Throughout their lives, students will interact and analyze both versions of multiplication arrays. But how do we get them to start seeing them as representations of math?
The 3-Step Approach to Multiplication Arrays
Wouldn’t it be wonderful if you could just say, “math is everywhere,” and POOF students can see the math patterns around them? Unfortunately, as we all know, students won’t just believe that math is everywhere. For many learners, seeing is believing.
In my classroom, convincing students that multiplication arrays are everywhere began with a discussion. A simple discussion often gets them thinking in new mathematical ways.
First, we talk about what we already know about multiplication. Their background knowledge depends largely on their grade and math experiences. Students often pinpoint:
- Multiplication is adding the same thing over and over again
- Multiplication is when you have more than one of the same thing
- Multiplication is when you times a number by another number
Then, we discuss ways we might show multiplication. This is when students might get stumped. Often, one or two students share that you can show multiplication with a specific type of manipulative. Students who have more experience with multiplication might reference examples from their own lives. For example: “When I go shopping, and we buy three cans of soup. That’s three times one.”
Now, it’s time to explore.
Step One: Multiplication Arrays in the Classroom
When introducing a large, real-world concept, I like to start with our micro-world: the classroom. The classroom is a contained space where students can easily find and present multiplication arrays to their peers.
So, we start by focusing on the classroom. Sometimes even just a wall.
I ask students, Where do we see multiplication arrays in this section of our classroom?
Get ready for a lot of hands.
Throughout my years doing this exercise, students typically found multiplication arrays often in a range of places, including:
- Windows
- Cubbies
- Material bins
- Rows of desks
- Work Displays
- Books on bookshelves (Note: check the number of books in each row)
If you’re starting with a wall, I highly recommend one that includes job charts, center rotation charts, and other wall resources that may also be in the form of an array.
When launching this activity, I am very specific with my language. Rather than using the question starter “Do you see…”, I use “Where do we…”. This acknowledges that there are definitely arrays to be seen.
Step 2: Multiplication Arrays Throughout the School
You’re at a pivotal moment. Students are becoming more aware of multiplication arrays. They have seen proof that they are present in our own contained space.
But, now what? Now it is time to transfer this knowledge. Because, after all, I want students to notice math everywhere. Not just the classroom.
Next Stop: The Whole School.
This step takes additional scaffolding (for the sake of everyone in the school community!) We begin as partners or as a whole group. As students walk through, I ask students to notice the arrays. When in partners, they record their findings. They can either draw/sketch their findings or write them down in a list. When we walk as a group, students “mentally collect” what they notice. They raise their hand and point it out to the whole class.
After we full walk through the school, we share! Trust me: You will be surprised by the number of arrays students find.
- Bulletin boards
- Signage
- Lockers
- Tiles
- Ceiling Tiles
Step Three: Multiplication Arrays at Home
By now, most students should be convinced that they can find a multiplication array beyond the classroom walls. In fact, many students will be excited to keep discovering arrays anywhere they can. Capitalize on that excitement! Take this activity one step further: a scavenger hunt at home.
Home multiplication arrays scavenger hunts can take on many different forms.
- A conversation starter with caregivers
- An in-class discussion
- A visualization and drawing activity
- A homework assignment, if your district requires homework
In this final stage, I ask students: Where do you see arrays at home? This question could be posed as homework, or students could visualize their homes and name arrays that they can remember. Challenge students to explore and discover arrays in their own homes and the world outside the school. You are guaranteed to hear excited cheers of “I noticed that _________ was an array!” Here are some of the many arrays students have shared over the years:
- My baby sister’s quilt
- The eggs in the egg carton
- The pictures hanging on the wall
- The pictures of tv shows on Netflix
One of my students came in after a long personal scavenger hunt announcing that they even found an array in the freezer: the ice cube tray!
What Next for Multiplication Arrays?
The multiplication arrays scavenger hunt is an amazing way to kick off a unit on multiplication arrays and get students to notice math in their daily lives. However, teaching and practicing the use of arrays doesn’t stop there.
The next step is to continue practicing work with concrete and visual representations before jumping into verbal and symbolic representations of multiplication. To do so, I rely heavily on my favorite hands-on activities. Here are two of my favorites!
Array Capture
Array capture is one of my favorite partner-work multiplication center activities. Truthfully, of all the partner-work activities, this one is my favorite for supporting visual, symbolic, and verbal representation simultaneously.

The gameplay is simple, and students will have fun playing for hours if you let them. Here’s how the game is played:
- The first player rolls two dice. Those numbers are the dimensions of their array (For example, the student rolls 3 and 6. They will build an array measuring 3 by 6) in which they color (each player has a different color) and write the equation. On the first roll, players must place their array in the starting square. However, all future arrays only need to be touching an existing array on one side.
- Next, player two rolls next and continues in the same fashion, but from their corner. If players cannot create an array because there is no space left, they lose a turn.
- The player to capture the most squares wins!
Added bonus: Array Capture is an activity that can be easily differentiated by swapping out sets of dice. I let my students choose the dice they want to play with– only rarely needed to “suggest” a more difficult or simple set. My students just learning multiplication usually select a set of dice that has only numbers 1-4, whereas other students may challenge themselves with numbers 5-10.

Multiplication Centers Mega Pack
Building with Array Tiles
Building arrays with square tiles continue to conceptual construction of multiplication. While our scavenger hunt helped students see math in the real world and learn how to identify arrays, using square tiles requires students to start thinking about the components of multiplication. It is a great hands-on way to teach multiplication at the very beginning and as we move into thinking about factorization and multiples.

I find it a particularly effective way for two reasons:
- It is a hands-on method that uses one-to-one correspondence.
- Multiplication arrays with tile squares are a visual representation of the relationship between multiplication and repeated addition.
Multiplication arrays bring math to life in a way that excites students. They are living proof that math can be seen. I hope the multiplication array scavenger hunt helps you kick off a multiplication unit that supports all of your students. Have another trick to differentiate multiplication instruction? Let me know in the comments!









Leave a Comment