Welcome back to our deep dive into mathematical representations! Today, I’m really excited to talk about visual representations and the WIDE variety we may see from our students. First, let’s do a three-sentence recap of this series so far:
Last time, we focused on concrete representations and the immense value of manipulatives. We also discussed some misconceptions that arise when teachers don’t have a deep understanding of the Concrete-Pictorial-Abstract model (sometimes referred to as CRA model). Finally, we began looking at a different model that makes the perfect companion to the CPA model, as it highlights a range of representations and stresses the importance of making connections between representations. It’s called Lesh’s Translation Model.
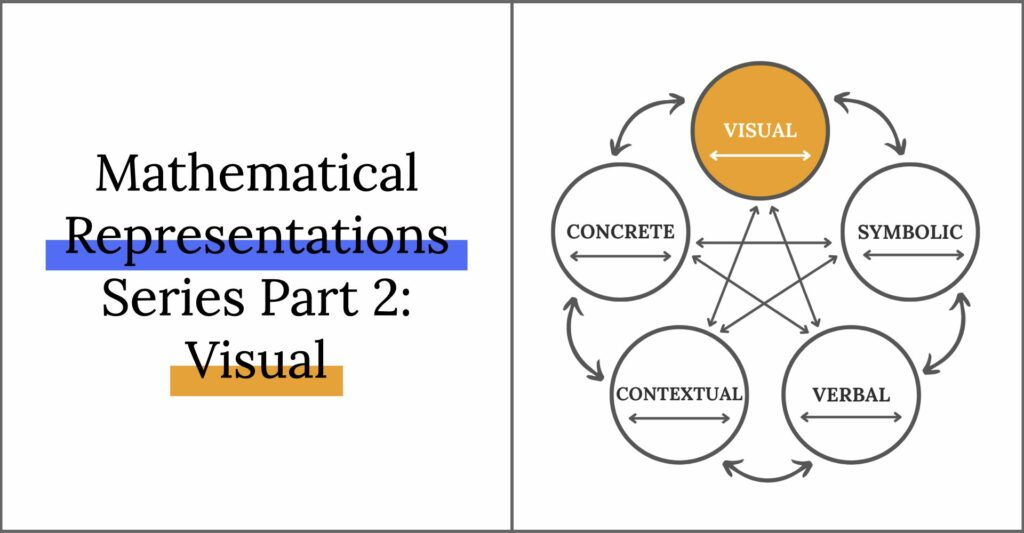
Visual Representation
Now, that we’re all caught up, let’s take a peek at Visual Representations. Sometimes this is called pictorial, semi-concrete, or representational.
This is when a mathematical concept is represented using visuals (whether that be drawings, diagrams, or charts). These visual representations can stand in place of concrete visuals, but don’t have to. They demonstrate that students can visualize a math concept, but also communicate it to others in picture form.
Examples
Let’s go back to the example from concrete representation. In that example, the student counted 5 yellow counters, and 4 red counters, and then determined that there were 9 counters altogether.

There are many ways that a student could represent this concrete model visually. One of the most basic ways would be to sketch their concrete representation. Here they’re coloring the red and yellow circles to visually represent the counters.

Now, the magic of these representations does not happen by creating them in isolation. Students deepen their understanding when they are able to make connections between different representations.
In this example, the student deepened their understanding by connecting their physical manipulative representation to a drawing they created to visually represent those manipulatives.
Connecting Two Visual Representations
We just mentioned that the most important part of these representations is encouraging students to make connections between them. We’ve seen how to connect concrete and visual representations, but we can also connect a visual representation to another visual representation. (Try to contain your excitement! Ha!)

In addition to their sketch, which is a more concrete visual, the student could use a more abstract visual like a number bond to show the idea of 4+5=9. Both are considered a visual representation, although one representation leans towards concrete, and one leans towards abstract.
When a student is able to connect the two different visuals expressing the same idea, they have connected this representation to itself and further deepened their understanding!
Some other visual representations the student could have used include a bar model, a number line showing jumps, or drawing the images on a ten frame. Just like there are countless ways to show this concept with manipulatives, there are countless visual representations our students could create. Our job is to encourage the creation of representations and facilitate connection-making between them.
WHAT’S UP NEXT?
This series is going to dive deep into each of the representations discussed in Lesh’s Translation Model, and then we are going to put it all together so we can make a big impact on your math teaching this year.
If you missed Part One about Concrete Representations, CLICK HERE to make sure you have all of the info you need before we move on!











Wow! I LOVE your posts! Thank you for helping math make sense.