Mathematical Representations Series: Putting it All Together

In my last five posts, I’ve gone a DEEP dive into Lesh’s Translation Model and Mathematical Representations. In case you’ve missed any of the representations along the way, be sure to check them out:

• ​Concrete​
• ​Visual​
• ​Symbolic​
• ​Verbal​
• ​Contextual

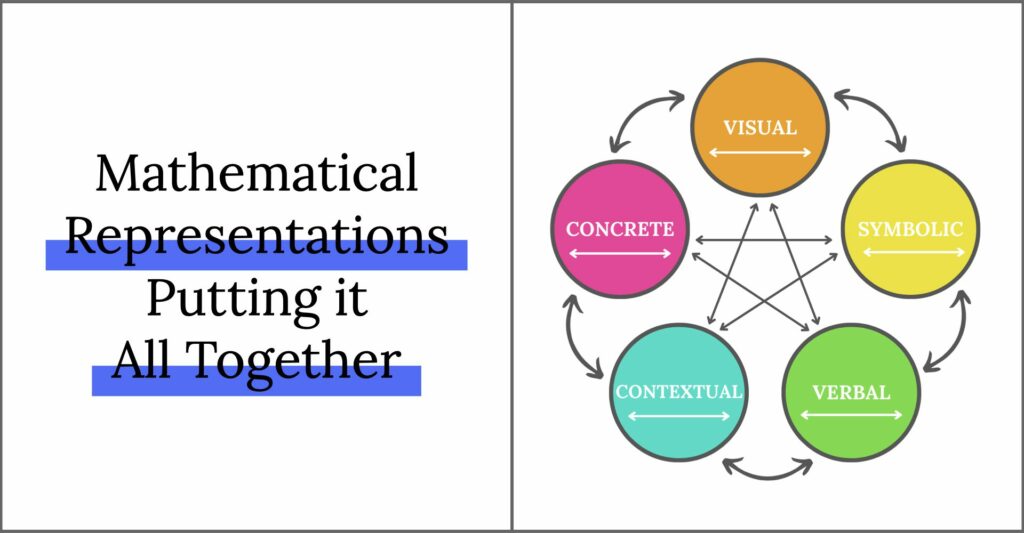
It’s great to understand each of these mathematical representations in isolation, but the magic happens when we encourage students to make connections BETWEEN the representaitons. We want them to create a concrete representation and be able to talk/write about it. We want them to create a visual representation and be able to show that same understanding symbolically. And we definitely want students to be able to understand any of these representations given real-world context.

Mathematical Representations in the Classroom

Now that we have an understanding of the 5 different mathematical representations, HOW do we actually go about doing this in a purposeful way in the classroom?

When we are planning our lessons, it’s important to think about how we can incorporate connections between representations. How can we actively seek out ways to have students build, draw, talk, write, and give context to their work? 

Don’t get overwhelmed. I am NOT suggesting doing ALL five in each lesson. No, no, no. But choosing two or three and supporting the translation between the representations will help deepen your student’s understanding of the content. And different lessons will naturally lend themselves to certain representations. These don’t have to feel forced.

Be Explicit

One great way is to be explicit and have common language around these mathematical representations. Name them with your students! It doesn’t have to be complicated.

As we naturally discuss different representations in our day-to-day lessons, we can pause and name them.  We can say:

• “What we did just now was use a drawing to help us think about the numbers we’re working with. The drawing helped us see the numbers so we could add them together.”
• “Did you notice that when we decided to build the number with our Unifix cubes we could see which number was greater than and which number was less than the other? Building each number was a great strategy because it made comparing them easier.”
• “The numbers made more sense when they became cookies. When we talked about subtraction as ‘eating the cookies’ we could picture what that meant.” 

When we are explicit, we can help students recognize the power of the representations and help them recognize them as a tool to understanding.

I hope this series has been helpful for you! I love talking about mathematical representations, especially relating to Lesh’s Translation Model. If you have any questions or connections, please let me know in the comments!