
I am so excited for this Summer Math Series to start! I’m beginning with one of my favorite concepts to teach: Number Sense! More specifically, I want to take a look at building fluency with composing and decomposing numbers.
The ability to fluently compose and decompose numbers is a critical step in mathematical thinking. It’s important to regularly provide a variety of experiences to help students increase their fluency, and think flexibly about numbers.
You’re saying, ‘well that’s great Jillian, but I don’t have time to plan those experiences, prep all of the materials, differentiate to meet the needs of all learners, and assess for student growth!’ Trust me when I say, “I FEEL YOU!”
That’s why today I want to do the following to help make this as easy to take back to your classroom as possible:- Explore some of my favorite LOW-PREP centers and activities
- Share how recording pages hold students accountable for their learning, and help you monitor their understanding
- Describe how to easily differentiate each center
- How introducing choice can both engage your students and decrease your planning time
- Share a quick and easy assessment to use at every level in your classroom
Begin with a Quick Assessment

Being able to assess your students quickly and at any point during your math block is such a luxury! That is why I LOVE the “In the Bag” assessment!
“In The Bag” goes by many names. You can use a bag, cup, or even just your hand- the idea stays the same. Essentially you are looking to assess a student’s ability to provide the missing part of a whole. For example, take a look at the picture above. I have six cubes and hide some in the bag. By seeing four cubes outside of the bag, they need to identify the number two as the missing part. I quickly put the cubes back in the bag, and pull out a different number to see if the student can identify a new missing part.

Kathy Richardson refers to this activity as the Hiding Assessment. Beginning with the number 4, the teacher assesses that the student can fluently provide the missing part for all combinations of 4. If the student can quickly provide each missing part, the teacher can move on and assess their fluency of the number 5.
The teacher continues to move through numbers, checking the student’s fluency at each number. When a student can’t fluently provide the missing part, that becomes the students “working number.” For example, if a student cannot provide 4 as the missing part of 6 when 2 is shown, 6 becomes the student’s working number. That student will then engage in a variety of activities that help them practice combinations of 6.
Easily Differentiate Each Activity with Dice
After you’ve assessed your students, you can provide them with a wide range of experiences to build fluency with their working number. Today I want to show you a variety of activities that are easily differentiated just by using different dice! That’s right- ALL YOU NEED IS TO CHANGE THE DICE!

Okay, so I may have a slight obsession with dice. About six years ago, our math specialist came into my classroom with a plastic container. It had previously been used to sort magnetic letters, but she had transformed it into a math dream! I knew I needed one for myself!
How do you use these dice to differentiate your activities? It’s easy! If a student’s working number is 5, they play each of the activities with a dice numbered 0-5. If their working number is 7, they use a dice numbered 0-7 or 1-6. This way all students can play the same activities, but each student will only be accessing numbers that can be used to compose their working number.

Math Centers to Teach Composing and Decomposing
Here are some of my favorites (all low prep, hands on, and can be done independently or with a partner).NUMBER TRAINS

Number trains are a great way to help students physically build parts to create a whole. To start, students need to roll a die (with numbers matching their “working number” parts). Let’s say a student’s working number is 5. If the student rolls a 3, they need to build a train of three cubes, ALL THE SAME COLOR. Next, the student must determine how many more cubes are needed to create a train of 5. The student then snaps 2 cubes together of A DIFFERENT COLOR to represent the missing part. They then write the sentence 3 + 2 = 5 on their recording sheet.
I like using recording sheets at centers. I find they are a great way to hold students accountable for their work while I am working with small groups. Also, checking them after the math block helps me monitor their understanding!
You can grab these Number Train Recording Pages [HERE]

Having two different color cubes available is crucial for this activity. It helps students identify the two separate parts needed to make the whole. I keep my cubes in bins already sorted with two colors in each bin. It makes it much easier for students to collect their materials, and provides an embedded reminder to use two colors.
*TEACHER TIP: Sorting cubes into your city’s team colors gets my students motivated. Red and Blue for the Patriots or Red Sox, Green and White for the Celtics, and Black and Yellow for the Bruins. I can’t tell you how much this little detail has helped engage my kiddos!
SPILL THE BEANS

Spill the Beans is a fun activity that is VERY low prep! All you need is a cup and some of these little white and red bean manipulatives. If students are working with the number 7, they should have 7 beans in their cup. For each round, the student needs to “spill the beans” from their cup and identify how many landed on the white side and how many landed on the red side. Students then write their math sentence on the recording page.
You can grab these Spill The Beans Recording Pages [HERE]

Addition & Subtraction Pack
SPILL A SENTENCE

Spill a Sentence is essentially the same as Spill The Beans. I just like having multiple activities for students to choose from. Some students like the beans, others like the counters. It’s nice to have both available to them at all times.
You can grab these Spill A Sentence Recording Pages [HERE]
CLIP A SENTENCE
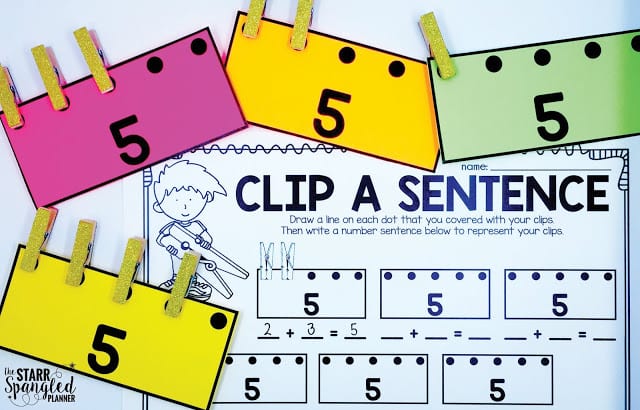
This center was inspired by all of the little clothes pins I find on the floor of my classroom. We use clothespins for everything from segmenting sounds to making tissue paper butterflies. Why not use them in a math center too?
Students grab the bin with their working number (the number cards, clothes pins and recording sheets are all together). I use this center to help students both compose and decompose numbers:

ADDITION: Have students roll a dice or use a spinner to determine how many clips they should put on their number card (If the students are working with “5”, they should use a dice or spinner with numbers 0-5.) If the student rolls a 2, they place 2 clips on their card. There are 3 dots remaining. The student records the sentence 2 + 3 = 5 on their paper.
SUBTRACTION: Have students place a clip on each dot on their number card. Then the student rolls the dice. (Again, if the students are working with “7”, they should use a dice or spinner with numbers 0-7, or 1-6.) If the student rolls a 4, the student must remove 4 clips from the card. There are still 3 clips remaining. The student records the sentence 7 – 4 = 3 on their paper.
You can grab these recording pages and number cards [HERE]
]GO FISH TO [WORKING NUMBER]

Go Fish is a well known game. Just throw in some Ten Frame cards and you have yourself a center! Let’s say a group of students are working on composing and decomposing numbers to 6. Those students will only be playing with cards 0-6. How do you play?
- Pass out 5 cards to each student (3-5 is ideal), and place the rest in a pile at the center
- Student 1 has a 2 in their hand, so they must identify 4 as the missing part to make 6. Student 1 asks one of their peers, “Do you have a 4?”
- If student 2 does have a 4, they must give their card to Student 1. Student 1 then takes the 2 and the 4, and places them face up on the table. This counts as 1 point, and Student 1 may go again.
- If student 2 does not have a 4, they say, “Go Fish!” Student 1 must draw one card from the center pile. If this new card matches a card in their hand to make 6, they may place them face down but not until their next turn.
- The first student to use all their cards stops the game. The student with the most pairs at this point in the game wins.

Why use 10 Frame Cards? They are a constant reinforcement for combinations to 5 and 10, which helps develop strategies for mental math. You can grab a FREE set for yourself [HERE].
BUILD A FLOOR
Build a floor is one of my favorite activities from Kathy Richardson’s Developing Number Concepts! It’s so low-prep, but really helps students think about how to compose numbers. Also, this activity can be an independent center, or students can work in partners or small groups to compete to Build a Floor the quickest. Let’s take a closer look.
The student playing this game is working to build a floor to 5. They have their die marked with numbers 0-5. The student rolls a 2. They must place 2 blue cubes in the first column (see below).

The student continues to roll, each time creating a tower of cubes and placing them on the board. In the example below, the student rolled a “0” on their second turn, so they placed no cubes in that column.

Next, the student moves onto their red cubes. They must use these red cubes to complete a tower to 5. To do so, they roll the die. If the student rolls a 2, they have to check to see if they can use 2 red cubes in combination with one of the existing blue towers to make 5. In the example below, the student was able to use the 2 red cubes in the fifth column to make 5.

If the student is unable to make 5, they lose their turn. If they are working independently, they simply roll again.

A student wins this game by completing ALL of their columns and building a complete floor of 5. If the student is playing independently, they are simply finished with the activity and can choose to play again or move on to another. I like to have student record their number sentences either in the recording pages of Kathy Richardson’s book Developing Number Concepts, or in their math journals.
NUMBER SHAPES
Number shapes are arrangements of squares to represent numbers. The are used to help students recognize larger numbers because these shapes naturally support subitizing. Take the numbers 5 and 7 for example:

With the number 5, students can quickly recognize the arrangement as a combination of 2 and 3. Now look at the number 7. Students can quickly recognize the arrangement as a combination of 2, 3, and 2. They may also be able to recognize it as a combination of 5 and 2.
These number shapes are a great tool to help students build fluency with composing and decomposing numbers. Consistent exposure to number shapes helps students create mental models of numbers. By having these models in their minds, students can begin to visualize math problems. (e.g. if you ask a student to solve 5 – 3 = ?, they can visualize the number shape 5 and remove the bottom row of 3 to solve the problem.)

I loved using this as one of my regular centers in first grade. I created these recording sheets to help hold my students accountable for their work, as well as gain practice with writing addition and subtraction equations. You can grab them for FREE by clicking [HERE].
HANGING OUT WITH CLOTHES PINS
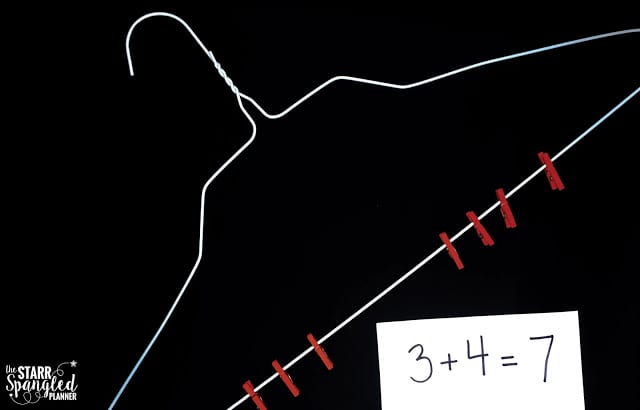
When I hear wire hangers, my mind usually jumps right to Mommy Dearest. “NO WIRE HANGERS EVER!” Well, I have news for you Joan Crawford- Wire hangers are a great tool for teaching composing and decomposing numbers!
I love a center that can develop math and fine motor skills at the same time! It also gives me something to do with all of the wire hangers we get from the dry cleaner! This center is quick to set up (all you need are hangers and clothes pins) and you’re good to go. My students like to write their number sentences on strips of paper and take pictures to document their work. When that’s not an option, I have them record their equations in their math journals.
INTRODUCING CHOICE
The centers above are always present in my classroom. Regardless of a student’s working number, they are all engaging in the same activities. I found that when I assigned students to specific activities, they would sometimes tire of doing the same thing. When my math specialist suggested I allow students to choose which center they wanted to try with their working number, my stomach flipped upside down! But my beautiful choice board!?! Am I even able to relinquish that amount of control? (Let’s be real- I love control!)
It took some serious convincing, but eventually I said, “okay, I’ll try it!” I had every intention of trying it for a day and throwing in the towel. There was NO WAY this could work! However, I have to swallow my pride, and admit when I am wrong.
Introducing choice to our Composing and Decomposing Centers was amazing! My students were far more engaged in their learning, and were much more willing to work collaboratively with their partners. They were having meaningful conversations about the math work in front of them, and building off one another’s observations.
Another plus? I no longer had to make my little charts that carefully planned where each student was going at every center all week! Decrease planning and increase student engagement? Win, Win!
You can grab many of these activities by clicking on the photos below!


Make sure to stop by next Monday! We’ll be talking about Math Word Walls and how to use them effectively in the classroom!












So many awesome activities and games here, Jillian! Thanks for sharing such awesome resources!
This is an awesome post with so many great activities. Do you have other math centers going at the same time or are these the only choices your students have? Do you limit the number of students at each activity? Thank you so much for all this great information.
Hi Molly! Thank you so much for your kind words! I'm happy to know there were some nuggets in there for you. As for my set up, I have this collection of activities as one center called Working Number Choice. It is a year long center that remains even while we are covering different topics in their guided math groups. Therefore only about one fourth of my students are using these centers at a time. The others are either meeting with me, writing in their math journals, using technology, or engaging in an activity that is directly related to the content of their guided math group (eg telling time, graphing, coins…) I haven't found there to be any issues with sharing supplies with this set-up. Does that make sense?
This post is packed full with great ideas. Love it! The link for the number shapes doesn't seem to be active, though.
Thank you! I just pulled it down temporarily to bundle them together for an easier download! Hope to have it up by tomorrow!
Do you know when we will be able to download the number shapes recording sheet? I have purchased the other bundles.
I am out of town until Friday, but the recording sheets are all ready and will be uploaded this weekend! Thank you for your patience. Balancing a newborn and a blogging life is proving trickier than I anticipated 🙂
I'd love to use the number shapes activity. It would fit in perfectly with what I'm doing now! I have already purchased your packet- and I love it.
I love the ideas, However, I teach third grade. Is there a Differentiating center for 3rd grade?
Or do I modified the activities for third grade
Hi. I loved all the ideas above. Thank you . I would like to aske you if you have an idea or an exercise to do with a child at the first grade who had difficulties with the numbers sequences . Thank you
Where do you find your non-traditional dice that are less than 6 dots? Did you have to make them?
Hi Stacie! Yes, I purchased blank dice that have stickers. I draw dot images on the stickers and then place them on the dice. I hope this helps!
Thank you! Thank you! Thank you!
What a wonderfully informative and inspiring post. My renewed understanding of math concepts along with your fantastic activity ideas, are going to make my lessons much more effective and fun.
Oh Gail!
Thank you so much for taking the time to write this. You’ve officially made my day. I’m so glad this post was helpful, and you think it will make a positive impact on your teaching.
Warmly,
Jillian