
Open number lines are the Swiss Army knife of number lines: useful, practical, and multi-purpose!
One way to use open number lines is to use them as a model for addition and subtraction. Unlike regular number lines, open number lines are created by the mathematician. “Open” in the term open number line means that it does not have a set start and end point. Instead, students decide where to start and how to decompose a number to add or subtract.
There are multiple ways to solve problems using open number lines, which allows students to approach problems in a way that makes sense to them. If you’re reading this and thinking, “A visual support that can be differentiated to the needs of each learner and also acts as a perfect tool to help students share their thinking?!” The answer is, yes, open number lines do it all.
But today I’m here to share the other side of this conversation. While open number lines are an incredibly versatile tool, I have found that students often stumble on a few common obstacles, which can make things frustrating for students and their teachers. Let’s face these obstacles head-on so that we can take full advantage of the greatness that is open number lines!
Obstacle #1 – Where to begin with open number lines?
Starting with open number lines from scratch can leave students scratching their heads! Because open number lines do not exist until students create them, the first obstacle kids encounter is how to know where to even start their number lines. Fear not, every problem drops a hint!
When solving addition equations, students should already have an understanding of the commutative property (even if they don’t know what it’s called!) so that they know that, for example, 45 + 76 and 76 + 45 will have the same sum. This property of addition is something students should be familiar with from their work with addition in first grade.
When creating their open number lines to solve 45 + 76, students can choose to start at 45 or 76 because of our old pal, the commutative property. When students first begin doing this work, it really will not matter which addend they choose to start at. However, as they progress, students will likely begin to realize that, like when they are counting on to solve problems like 4 + 7, it can be much more efficient to start at the larger addend. When using open number lines, starting at the larger addend like 76 will mean fewer jumps to get to the sum.
Here are two examples of what an open number line might look like for 45 + 76:
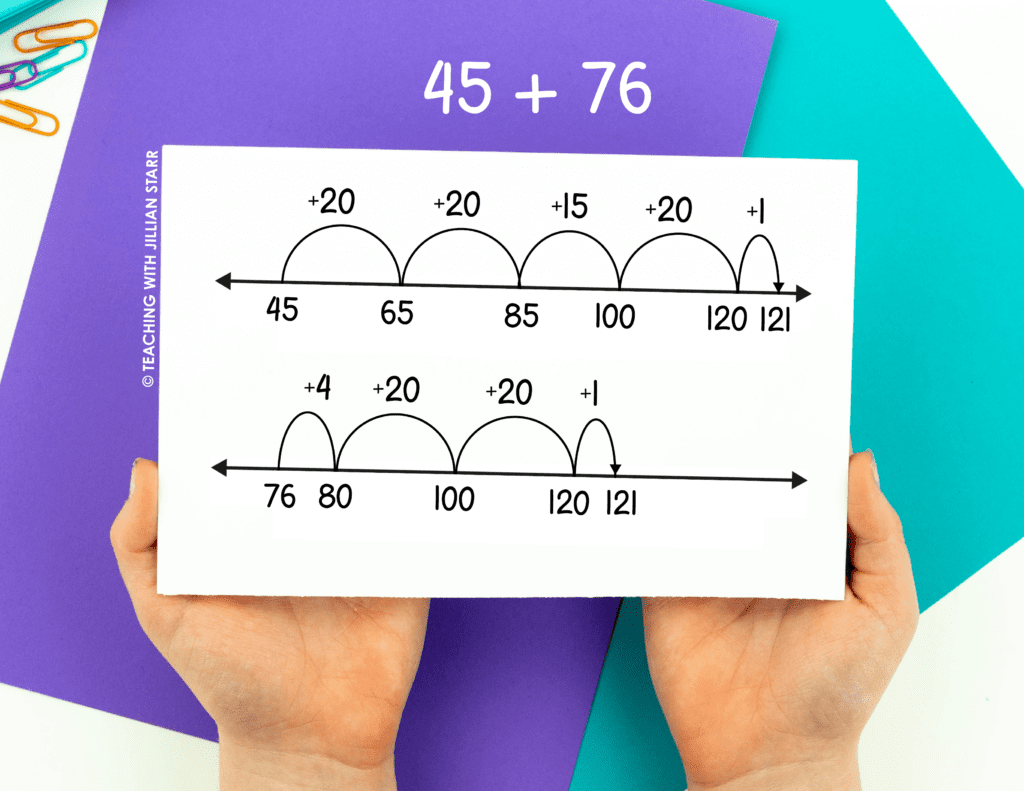
Of course, not all problems will be addition problems with two addends. Instead, students will have to solve problems like 82 – 34 and 35 + __ = 59. Subtraction equations can be approached using the idea of counting back to subtract. Students can start at 82 and jump back 34 on the number line to see where they land.

Similarly, missing addend equations Like 35 + __ = 59 can be solved by starting at the sum, in this case, 59, and jumping back 35 to see where they land.
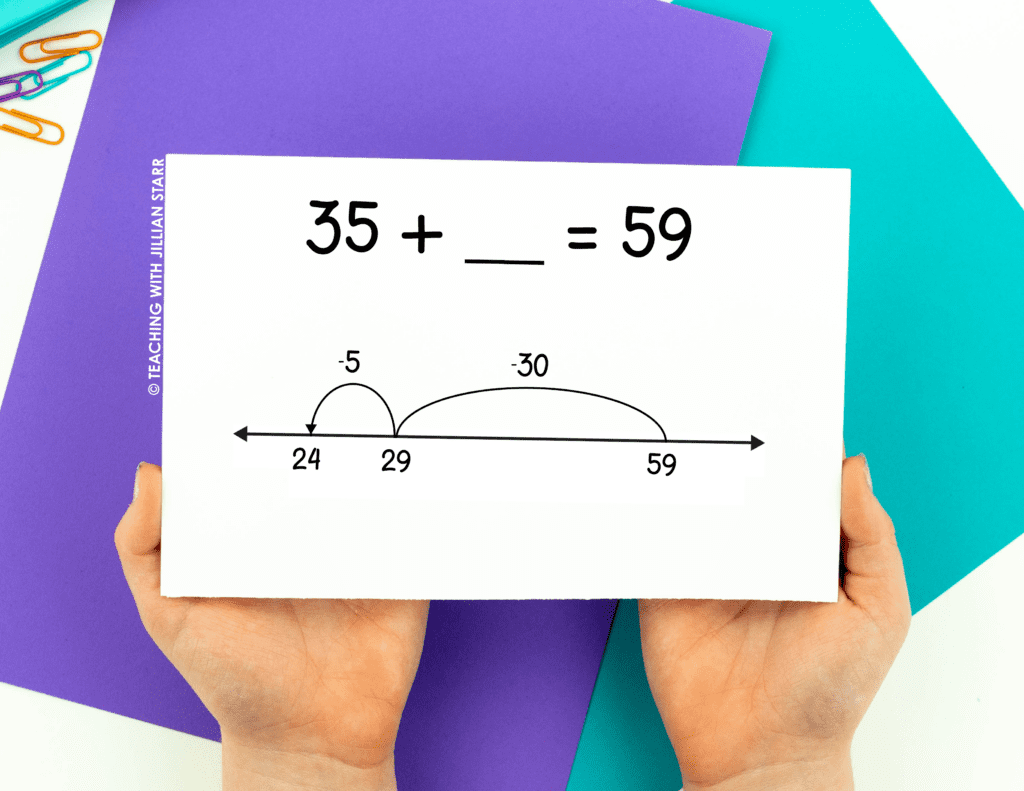
Those aren’t the only ways to solve those problems though! We want our students to understand subtraction flexibly. Subtraction is not only taking away, but also the distance between two numbers. So 82 – 34 can also be solved by starting at 82 and jumping back to 34. This time, the answer is not where we landed on the number line, but the jump it took to get there. Don’t worry – more on this later!
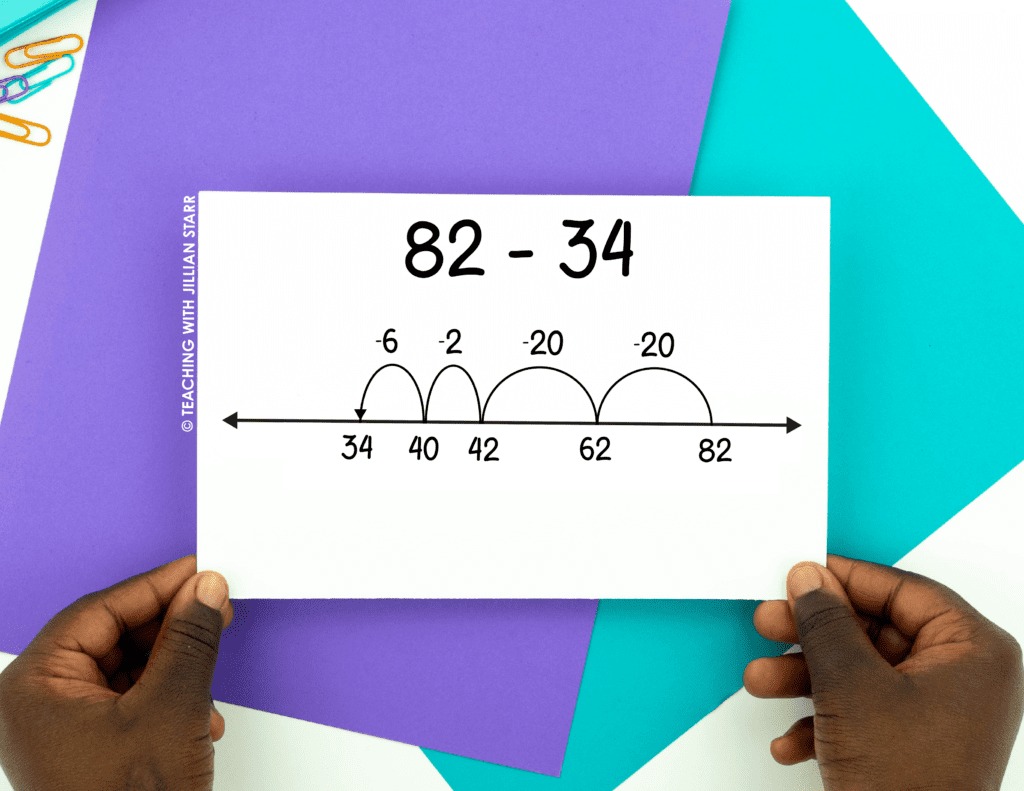
35 + __ = 59 can be solved that way too. Students can start at 59 and jump back until they land at 35. OR! They can start at 35 and jump forward until they land at 59. In either case, their answer is the distance between the two numbers.
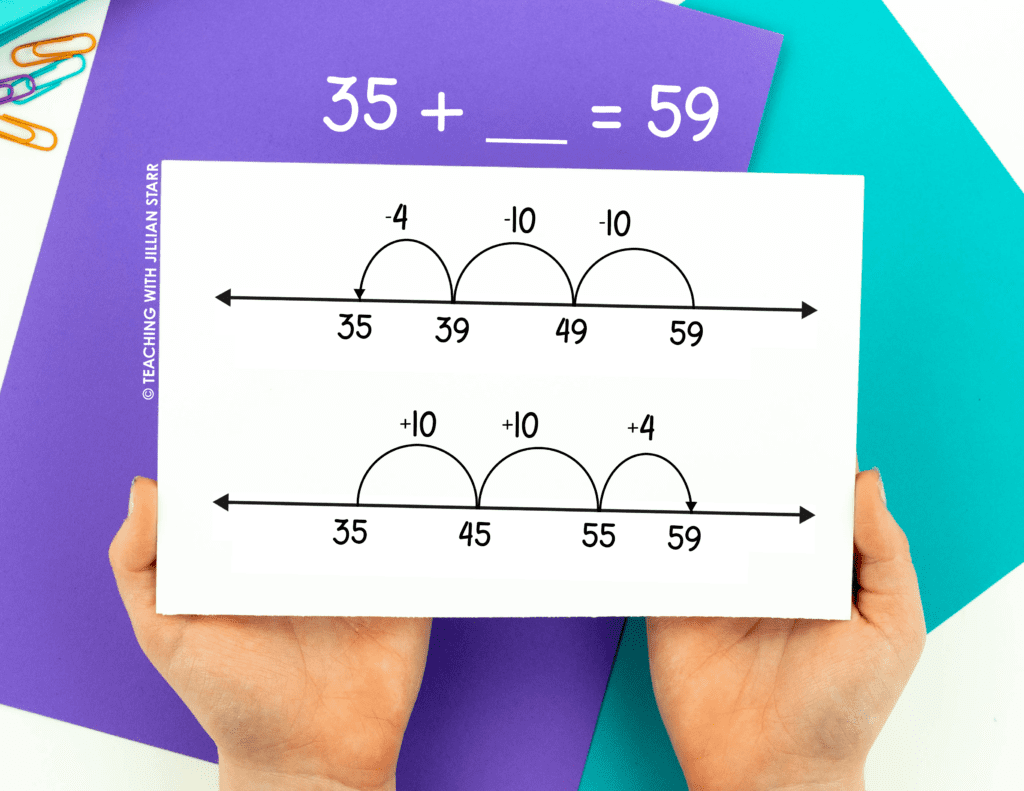
Now, I realize that I showed you, the teacher, how to model different problems on open number lines, but how do we get kids to think deeply about approaching these problems? Here are some prompts I use with my students when they are feeling stuck:
- What kind of problem are you solving?
- What information are you trying to find? (The sum, the addend, the difference, etc.)
- What if this was a smaller problem like 5 + __ = 9 instead of 35 + __ = 59, how would you solve it then?
- Tell me how you are thinking about solving this problem. How can we model that on the number line?
Obstacle #2 – Friendly numbers only on open number lines
The second obstacle I see students stumble upon is not using friendly numbers when moving on an open number line. “Friendly numbers” are what I call numbers that make computation easier. Not using friendly numbers can cause students to make calculation mistakes because they are attempting to add or subtract numbers mentally that they are not yet able to solve accurately, defeating the purpose of using an open number line.
Instead, we want to think flexibly about decomposing numbers to add or subtract them efficiently. Let me show you what I mean. Let’s say we are solving 57 + 28. Students who are not using friendly numbers might use the open number line to start at 57 and then jump forward 5 as their first step when adding 28. While 5 is often considered a friendly number, in this case, students need to add 57 and 5 which may be tricky for some students.
One way to use friendly numbers to solve that problem would be to decompose the 28 when adding to reach a multiple of 10. What does this look like? If we start at 57, we might first add 3 first to land at 60. Then I still need to add 25 but I can efficiently add a multiple of ten to a two-digit number so adding 60 and 25 is easy peasy.
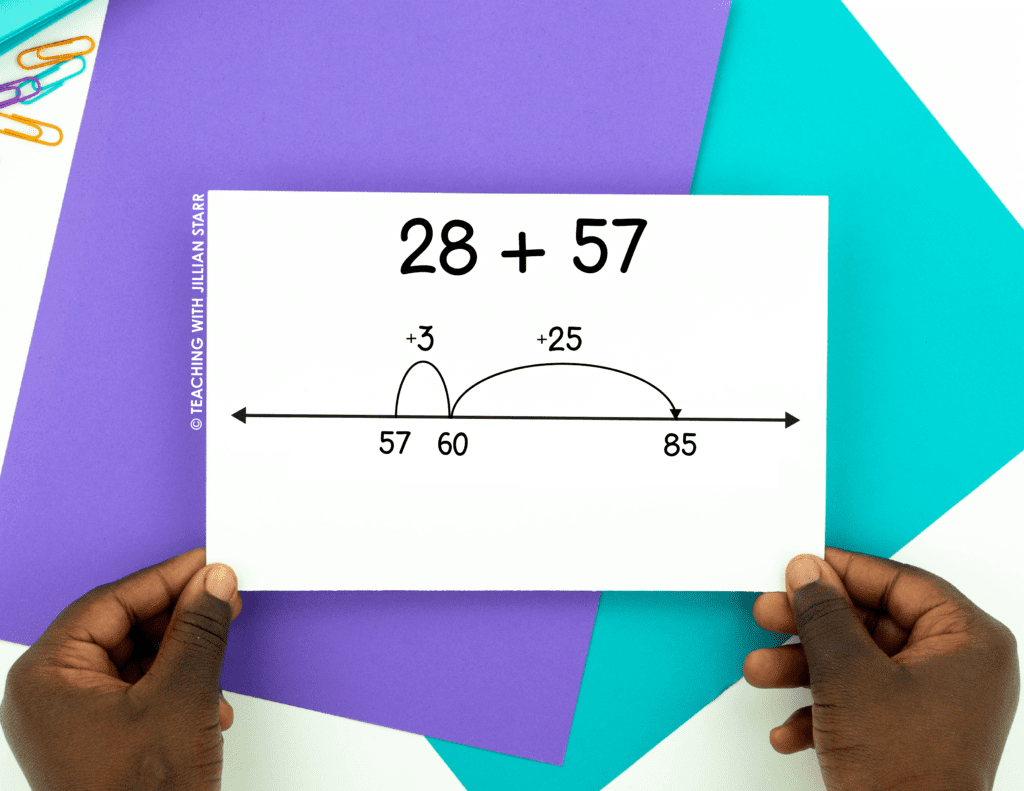
Using friendly numbers is also helpful when subtracting. Suppose a student is solving 72 – 26. As mentioned earlier, they could start at 72 and jump back 26, start at 72 and jump back to land at 26, or start at 26 and jump forward to 72. Regardless of the approach, decomposing the numbers to reach multiples of tens makes the calculations much more efficient!

Obstacle #3 – So what’s my answer?
Here is where it all comes together. Students have done all of the work using open number lines to solve the problem but then they’re faced with the million-dollar question: where is my answer? The final obstacle students face when using open number lines is figuring out what the heck the answer is! Is the answer the jumps, the number they landed at, where they started, or something else?
Some problems and approaches are easier for students. Problems like 45 + 76 tend to be straightforward when determining the answer. Students are often able to start at one number, jump on the number line, and find their answer at the spot on which they land.
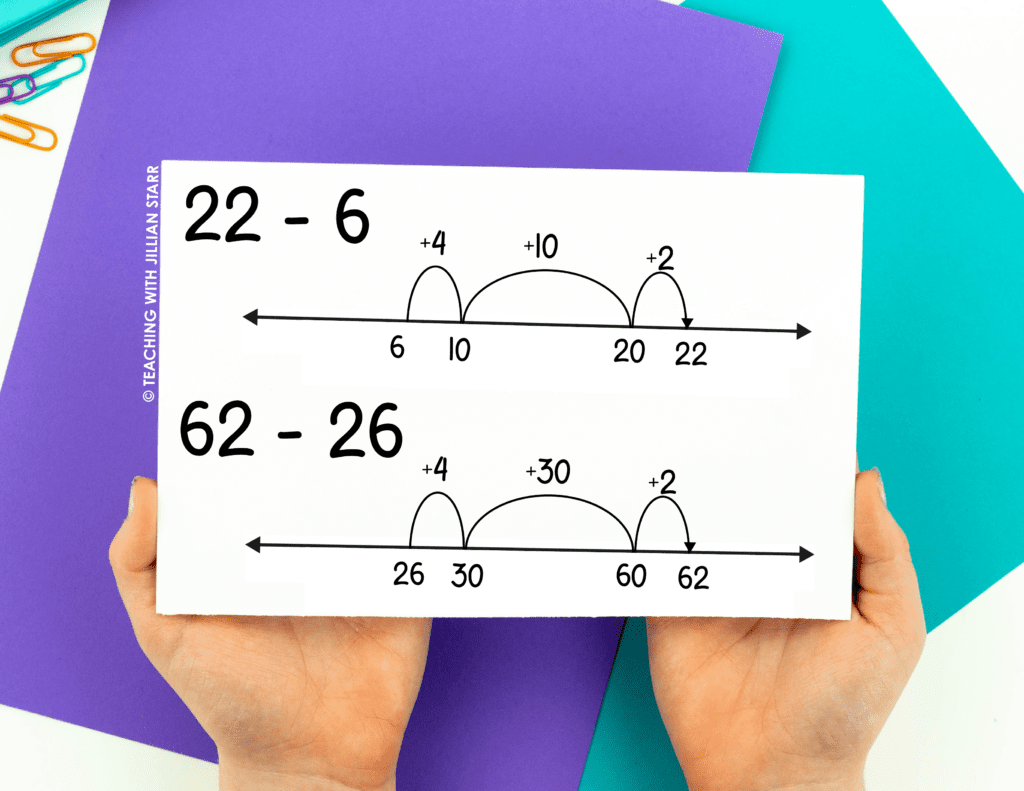
Some problems like 62 – 26 or 35 + __ = 59 are tougher nuts to crack. If students do not have a solid understanding of the properties of addition and subtraction equations those kinds of problems can create confusion. For example, a student who does not understand the meaning of the equal sign as “is the same as” rather than “the answer” may say the answer to 35 + __ = 59 is 59.
Another student who does not have a solid understanding of the relationship between addition and subtraction may attempt to solve 62 – 26 by starting at 26 and jumping to 62. In this case, the answer would be the total number of jumps it took to get to 62. In other words 26 + __ = 62 with the blank representing the jumps. However, without that important understanding, students may look at their open number line and say their answer is 62 because that is where they landed.
Smaller Problems to Larger Problems on an Open Number Line
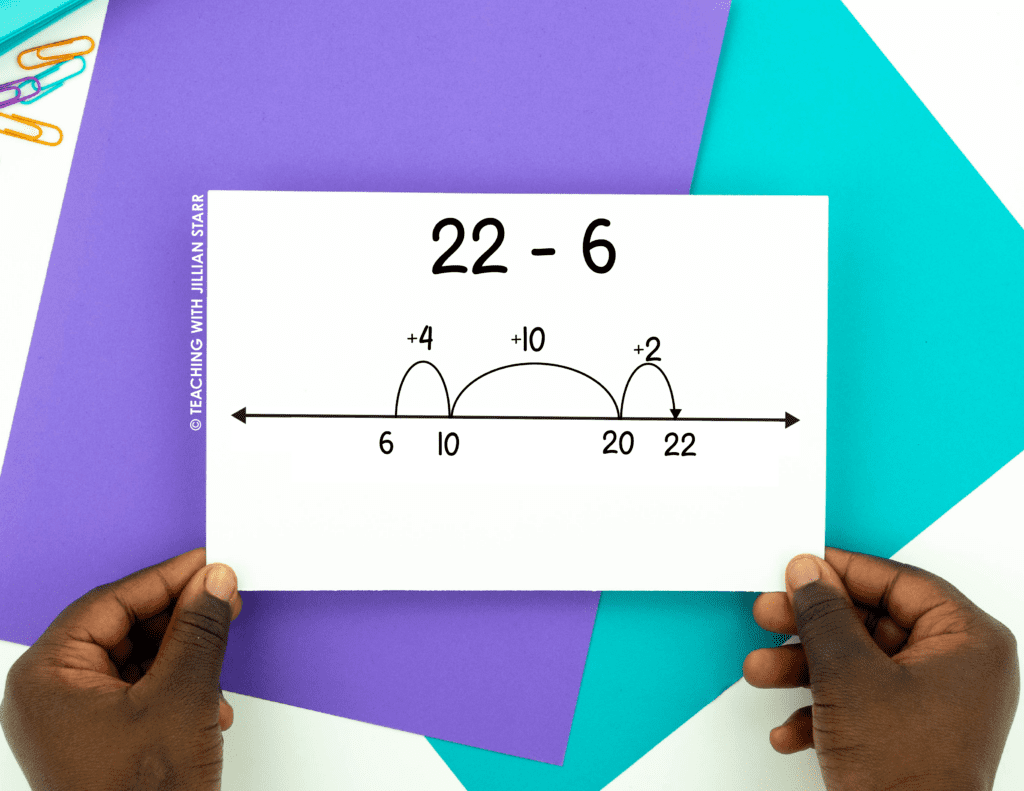
To support students who are facing this obstacle, it can be very helpful to have them solve similar problems using smaller numbers. Instead of solving 72 – 26, I might ask a student to show me how they can use open number lines to solve 22 – 6 using the approach they were attempting to use with the larger problem.
For example, I might help them to start at 6 and jump to 22 using friendly numbers. Then we’d discuss what the answer is to the smaller problem, 22 – 6. Once students are comfortable using their approach with these smaller numbers, I’ll have them work back up to the larger problem.
Some students often just need a simple reminder to look again at the problem they are trying to solve! For example, when solving 35 + __ = 59, students may just need the reminder to name the “mystery number” rather than one of the numbers already in the equation. I’ll ask, “Which of the numbers you see is the one that was a mystery when you first started solving?” Everyone loves a good mystery and this phrasing has resonated with so many of my students!
While second graders likely have experience with number paths and even number lines, the transition to open number lines can be tricky. Getting ahead of the common obstacles young mathematicians face will certainly help them to be successful along the number path to number line progression in no time!












Leave a Comment