Teaching Rounding to the Nearest Ten through Exploration and Real-World Context

I remember someone asking me if rounding to the nearest ten or hundred was “something students REALLY needed to know, or do we just teach it because it’s on the test?” It’s a fair question. Many skills don’t seem necessary until we really step back and look at that skill’s real-life applications.

As an adult, has anyone ever asked me the number of cookies I baked, and then round it to the nearest ten? No! (And not just because I don’t bake.) The skill in the context of answering a question is not something required in real life. However, we do use rounding all of the time to support estimation.

Rounding to the Nearest Ten in Real Life

Here are just a few examples of how I used rounding with estimation last month:

1. We went apple picking, and it was cash only. I used rounding to the nearest ten to approximate how many bags of apples and cider donuts I could purchase without going over the amount of cash I had in my wallet.

2. My youngest child spiked a fever, and I was trying to figure out how much medication we had left, or if I needed to get more before the next day. I used rounding to help work with her dosages (because infant dosages go into the hundredths) and estimate how many doses we had left in the bottle.

3. I went through my monthly subscriptions on my credit card bill (something I HIGHLY recommend doing). I took each line item and rounded it to the nearest ten to estimate how much I was spending on these monthly subscriptions… and then promptly canceled several of them!

4. My youngest has started climbing, which means she is getting into everything. I was tired of scrubbing crayon off the walls, so I went to IKEA to get one of those peg boards to house my older kid’s art supplies. I used rounding of centimeters to the nearest ten constantly while deciding how many panels and accessories to purchase in order to make something that would fit in our space.

There are countless other examples of rounding to the nearest ten, but these are the first that came to mind. I’m sure you can think over several too! The point is, rounding to the nearest ten is a very useful skill, because we use it constantly as we estimate.

Introducing the Idea of Rounding to the Nearest Ten

Now (hopefully) we are convinced that rounding to the nearest ten is a useful skill to teach, but then the question comes: how should we teach it?

If you know me, you know that I like to teach math through explorations. Rounding is no different! I have a great and engaging way for your students to gain a deep understanding of rounding to the nearest ten by allowing them to discover the rules of rounding on their own (and you as their guide).

Start with the Why Behind Rounding to the Nearest Ten

As I explained earlier, we use rounding to the nearest ten all the time, whether we realize it or not! Sharing these contexts with students can be really helpful in getting them invested in learning this skill. It also gives the skill context beyond the four walls of your classroom, which creates buy-in.

Creating the Context for Rounding to the Nearest Ten

Let’s take something they might enjoy like purchasing new books for the classroom. I like to have students submit books they’d like to purchase for the classroom for this activity, and bonus, we put them on a wishlist and send it out into our community later).

When planning for the lesson, I pull their book list and I write the prices next to them (I round to the nearest whole number- see! We’re using rounding already!)

Here’s an example (I put them in relative order of how far removed they are from rounding to the nearest ten):

• The Book With No Picture: $11
• Choose Your Own Adventure Box Set: $39
• The Sour Grape: $18
• Ada Twist Scientist: $12
• Dog Man Box Set: $37
• Watercress: $13
• Geronimo Stilton Box Set: $76
• Magic Tree House Books 1-28: $44
• Add more or less depending on your preferences

For this activity, I tell students that I want to ask for about $300 for books this year. We have a good list so far, but I want to know if we’ve already added too much, or if I can keep adding more.

The Introduction

I go back to previous number talks we’ve done where students share that their brains like working with tens! (Decomposing into tens and ones is always a student strategy during our number talks, and they support their strategy by saying that adding tens is just easier than other two-digit numbers. I’m using this as my anchor.)

“If our brains like to work with tens, do you think we could turn these numbers into tens (without all of the ones making things messy) so I can have an idea of how much these cost? I don’t need an exact answer. I just need to know if I’m close. I need an estimate.”

I look to my students to see what they think. I love to see the bottom lips get tucked under their teeth while their eyes look up in a deep state of pondering. I pull them in for an example.

“Okay, if I want to just quickly add tens in my head to get an idea of how much I’m spending, I have to change some of these numbers. If I wanted to change The Book With No Pictures to a price that is easy to work with, what price should I use?”

I love waiting to hear students’ answers. Some will say $10, some will say $20 and others might be unsure. We talk about how far $11 is from $20, and how far it is from $10, and then which seems like it would help us get a better idea of how much I’m actually spending (when I’m off by $9 or $1?). This is our segue into rounding to the nearest ten.

Whole Class Exploration of Rounding to the Nearest Ten

Above I mentioned that we talk about our $11 book, and which benchmark number makes more sense when rounding to the nearest ten, $10 or $20. How do we go about determining this together?

1. I draw a number line on the board with eleven tick marks.
2. I write the number 11 below the center tick mark.
3. I explain that we’re going to move out one number at a time on either side of 11 to see which direction will get us to a benchmark of ten first.
4. I write the numbers one more (12) and one less (10) on the tick marks to the right and left of 11
5. I circle the 10 and acknowledge that we have found the closest ten.

I ask them if they will help me find the nearest ten of some of the other book prices. We draw another number line (we don’t erase the previous one). We continue through several of the others together as a class so I can model using the number line a few more times.

I might ask if a student wants to come up and help with one and allow them to model using the number line. If this happens, when the student finishes, I’ll be sure to ask the rest of the class what they noticed to help reinforce the steps.

Individual/Partner Exploration of Rounding to the Nearest Ten

After we have gone through several examples as a group, I pose a wondering to the class: “I wonder if there is a pattern to this, or if it’s different every time?” I encourage us to test it out.

I pass out little number lines and ask students to pick a number between 20 and 80 to put in the middle of their number line. Then they go through the same process of moving out one number at a time until they find their first ten. (You can get these Rounding Number Lines for free HERE)

I let students round multiple numbers to the nearest ten and sometimes I create numbers in advance to make sure we have a solid variety of numbers. I don’t give a number that students have to complete. When we have what appears to be “enough,” we simply come back together as a group.

(If students try a number ending in 5 and discover that they reach two benchmarks at the same time, I ask: “Why do you think that is?” and then ask them to hold onto that thought to share with the group.

Discovering the Rule of Rounding to the Nearest Ten Together

Sorting Numbers

When we come back together, I ask the group if we can sort the number lines into two piles:

1. The benchmark is less than the starting number (e.g. the starting number is 34 and the benchmark is 30)
2. The benchmark is greater than the starting number (e.g. the starting number is 48 and the benchmark is 50)

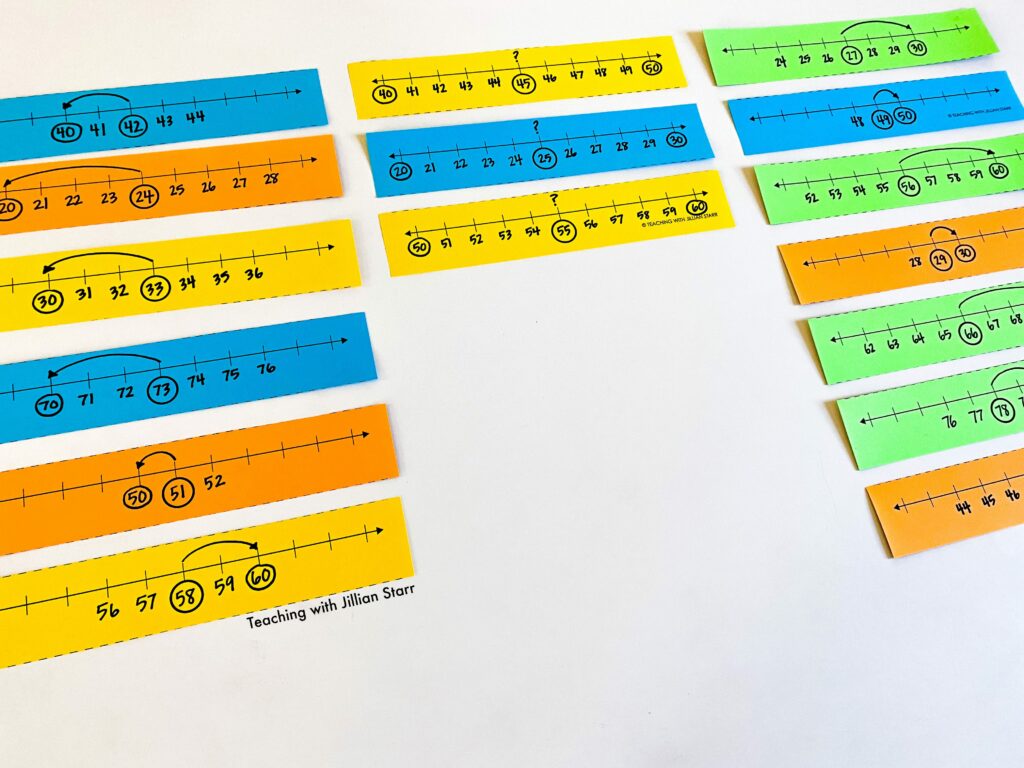
Students start sorting, and inevitably we realize that we need a third pile! Sometimes we found two benchmarks at the same time!

When the sorting is complete, I record what we found on chart paper.

Then we search for patterns!

Finding Patterns When Rounding to the Nearest Ten

I let students take a long hard look at the chart. I ask them to put their hand on their knee with a thumb up if they notice anything. This gives ample wait time to allow students to find the pattern for themselves.

When I see many thumbs, I ask students to turn and talk to someone and share what they notice. This is the fun part! The excitement that starts to build when students discover the pattern is awesome to watch.

“It sounds like y’all are noticing something here! Does anyone want to share?”

Together we name the patterns:

• Numbers 1-4 find the lower benchmark first
• Numbers 6-9 find the higher benchmark first
• 5 finds both at the same time

Defining Rounding to the Nearest Ten

This is when I introduce the language to support their discoveries. We name what they’ve been doing as “rounding to the nearest ten.” Rounding is simply when you change the number to the nearest benchmark number. Sometimes we round to the nearest benchmark of ten, sometimes the nearest hundred, or even the nearest million (depending on what numbers we’re working with).

When we round, we have discovered that numbers 1-4 round down to the nearest ten, and numbers 6-9 round up to the nearest ten. But what do we do with 5? (If you have time, ask them what they’d do… it’s fun to hear their ideas!)

I explain that the general rule in math is that 5 rounds up to the nearest ten. I give lots of examples of why this might be better to help put the idea in context:

• When we’re estimating how much money, it’s better to err on the side of caution so you make sure you have enough money.
• When you’re estimating how many supplies to buy for the class, it’s better to have too many than too few.
• When you’re sewing, it’s better to estimate too much fabric than too little (otherwise your clothes won’t fit).
• When you’re building a house, it’s important to have more wood than too little, or your house won’t be stable.

We could keep going all day, but we really want to help them understand WHY we generally round up.

Wrap-Up Rounding to the Nearest Ten

When we’ve finished our discussion, I make sure to set aside time that day or the next for students to help create an anchor chart to show their learning of rounding to the nearest ten. It always includes:

• The term “rounding to the nearest ten”
• The T-Chart with the different numbers we sorted
• A number line that shows how we found the benchmark numbers
• The rules regarding numbers 1-4, 5, and 6-9

This way, students have a visual reminder of our exploration and can continue to take ownership over their discoveries.

Important Contextual Discussions

We teach math so it can be applied in real life. Rounding to the nearest ten is a skill that we use frequently, but it’s also REALLY important that we know WHEN to apply it and when we shouldn’t.

Rounding to the nearest ten is used to help us estimate. It is not used to give precise calculations.

I like to brainstorm a list of times when should and should NOT use rounding. You might say, when shouldn’t we use rounding to the nearest ten? Well, here are three examples I frequently use with my students:

• Measuring how much medicine we should take. We are supposed to take an exact amount, and that shouldn’t be changed. Rounding up could make us really sick, and rounding down might make the medicine not work.
• Rounding up with time. If your bus comes at 7:47, you don’t want to get there at 7:50 because you’ll miss it!
• If you are following a recipe, you should not round up or down the measurements/amount of ingredients.

I hope this post has been helpful in rethinking how we can teach rounding to the nearest ten. Allowing students to find the patterns within rounding for themselves (instead of imposing an arbitrary rule) can be so powerful!